Tangled Polygons
2005/08/16
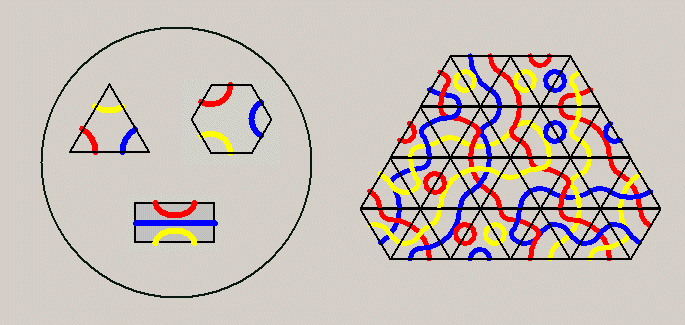
Take one of the above polygons and connect the six border positions by three paths, Due to
the different symmetry you get a different number of possible one-sided pieces for each polygon.
I colored the paths with three different colors or with three different colors out of four
increasing the number of distinct pieces a lot.
The table below shows the results. For three colors out of n
you have to multiply the second column by n!/3!/(n-3)!.
|
Number of pieces having three paths ... |
| Polygon |
without color |
with 3 colors |
with 3 colors out of 4 |
| Triangle |
7 |
30 |
120 |
| Domino |
11 |
48 |
192 |
| Hexagon |
5 |
16 |
64 |
Click on the cells to see the sets of pieces and some constructions made with them.
The main objective is to get matching colors for neighboring pieces. For the hexagons and the dominoes you can
also try to join all paths of one color in one single loop. If you take the sets with four
available colors sometimes for two of the colors single loops connecting all paths of each of these colors are possible.
Home

