
The number of distinct pieces can be determined if we look for all combinations of paths for
the dominoes and count how many colorings are possible for each path type. This is done for
three colors in the picture below. For three colors out of four all numbers must be multiplied by four.
For pieces with only one or two paths and no color have a look at
Ed Pegg's Mathpuzzle.
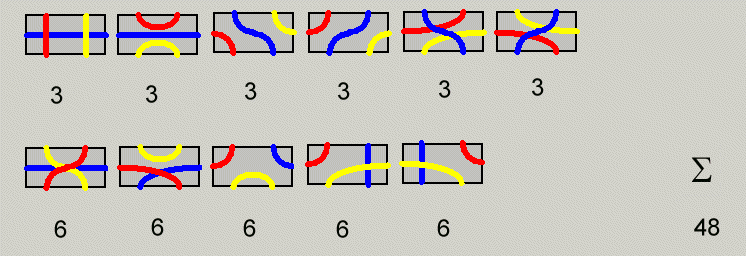
With 48 dominoes in the set the total area of the pieces is 96 unit squares.
Starting with a 10x10 square you can delete 4 unit squares in the center or at the corners
and cover the remaining area with the dominoes, where all paths of one color are connected
in one large loop. In the picture the red paths were chosen.
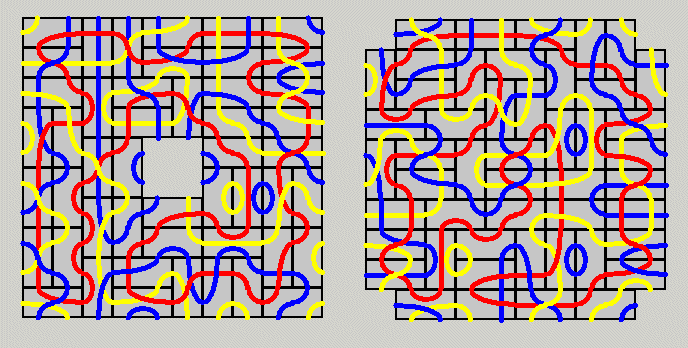
A 11x11 square with a 5x5 hole is possible, too and it is shown with real pieces.

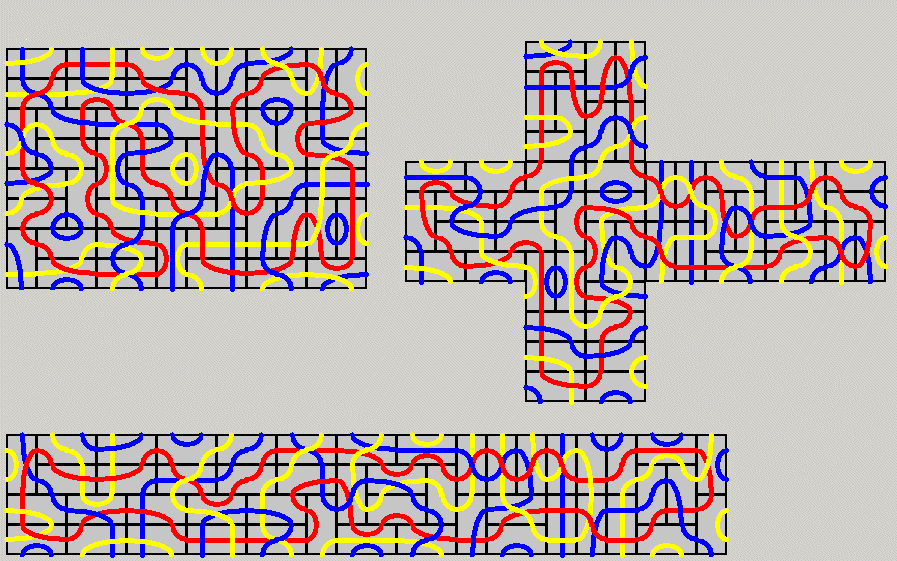
The area of 4-fold replicas of the hexominoes is 6x4x4=96 and therefore these figures give
another set of problems to solve. Three examples are shown the other ones are
here.
If we use three out of four colors, we get a set with four times as many pieces and you may try for
2-fold replicas of the figures already seen. It would be nice to have all paths of two colors
in two large loops. But these problems are very hard to solve. My strategy was as follows: Try to
find a solution for half the figure which can be rotated with an additional change of colors to get
the whole construction. The ring in the title and two rectangles were done this way. Unfortunately this method doesn't work for figures without rotational symmetry.

To display the constructions I cut 6cm x 3cm rectangles from plastic, stuck the paths on the front side and
little magnets on the back side. Now you can put the pieces on an iron board where they can easily be moved
around to get the different figures.

Index
Home







