
The number of distinct pieces can be determined if we look for all combinations of paths for
the triangles and count how many colorings are possible for each path type. This is done for
three colors in the picture below. For three colors out of four all numbers must be multiplied by four.

For triangles it isn't possible to gather all paths of one color in a single loop, because there are the little paths
connecting two positions at one side, which can only match another little path closing a loop.
But it may be interesting to ask for the maximum length of a loop or line, but I haven't tried yet.

Beside the shown symmetric figures it should be possible to make replicas of pentahexes. Three examples are given below.
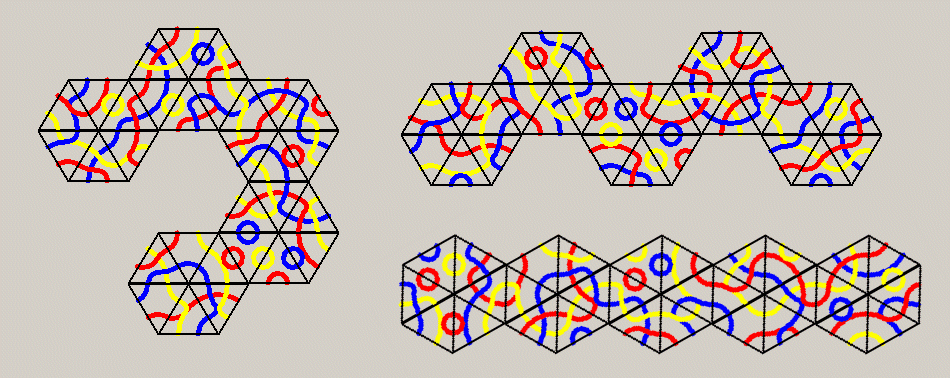
If we use three out of four colors, we get a set with four times as many pieces and you can
look for 2-fold replicas of the figures
already seen, but the constructions are more difficult.

Here are the 2-fold replicas of the same pentahexes as shown above.
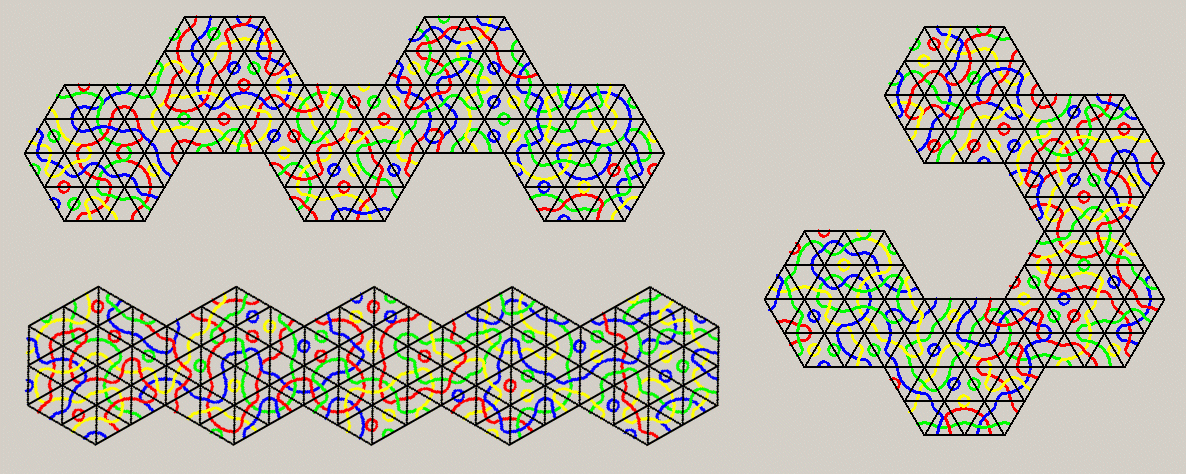
Beside the enlarged constructions there are some new figures that can be made. The size 13 triangle with a size 7 triangle
hole shown in the title is another example for this set.

Index
Home







