Hexagons

If you color hexagons with n colors at the six sides you get (n^6+n^3+2n^2+2n)/6 one-sided and (n^6+3n^4+4n^3+2n^2+2n)/12 two-sided distinct pieces.

Colors	One-sided Pieces		Two-sided Pieces
	Number	Examples	Number	Examples
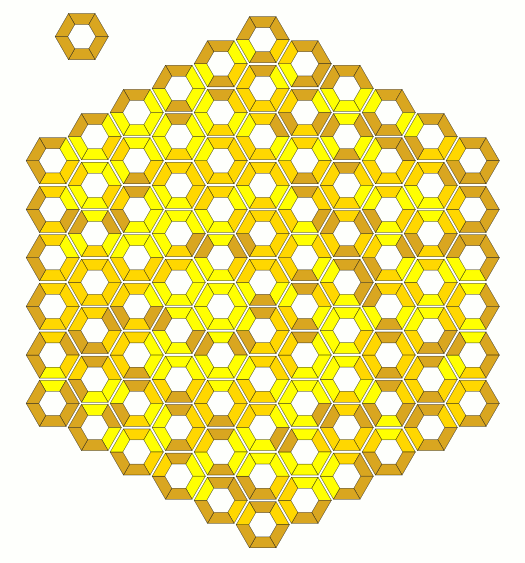
2	14	Tesselation of the Plane	13	Tesselation of the Plane
3	130	Rectangle, Trapezium, 13x10 Parallelogram, Two Rhombs, Hexagon	92	Rectangle, Trapezium, Rectangle with Hole, Hexagon
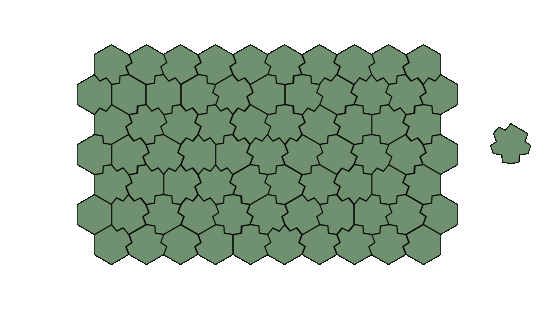
4	700	Truncated Triangle, 28x25 Parallelogram, 50x14 Paralellogram, Rhomb Ring	430	Truncated Triangle

Instead of colors you can choose different shapes for the edges of the hexagon.

A straight edge replaces one color and a pair of symmetric male and female edges replaces two colors. In this case the number of pieces remains the same but the constructions must be changed.

Symmetric S-shaped or Z-shaped edges match with oneselfs as long as the pieces are on-sided. Under this condition the pieces are essentially the same as the colored ones. For two-sided pieces it's different. If you turn a S-shaped edge upside down you get a Z-shaped one, whereas colors remain unchanged. I had a look at some sets of pieces with different combinations of edge shapes.

One-sided Pieces			Two-sided Pieces
Edge Shapes	Number	Examples	Edge Shapes	Number	Examples
ISZ	130	no difference to colored pieces	ISZ	74	Rectangle
IFM	130	Rectangle, Trapezium, 13x10 Parallelogram, Two Rhombs, Hexagon	IFM	92	Rectangle, Trapezium, Rectangle with Hole, Hexagon
ISFM	700	Truncated Triangle, 28x25 Parallelogram, 50x14 Paralellogram, Rhomb Ring	SZFM	382	Truncated Triangle with Hole
			FMfm	430	Truncated Triangle

2 colors, 14 one-sided pieces:

We can't get neither a hexagon nor a parallelogram with same colored border, because the number of pieces with two or more consecutive sides of this color is too small, but a tesselation with a symmetric figure can be constructed.

Jared McComb noticed, that the number of one-sided two-colored pieces without the single-color ones is 12 and suggested to tile the plane with irregluar hexagons composed of these pieces. Tesselations with those hexagons and parallelograms are shown below.

2 colors, 13 two-sided pieces:

For a tesselation with the two-sided pieces I used a trapezium, which was shifted and rotated.

At Gamepuzzles such a set with different edge types is available. A wonderful symmetric structure with beautiful colors is composed with this set.

3 colors, 130 one-sided pieces:

Constructions with different types of symmetry are possible.

Jared McComb suggested to discard the three single-colored pieces and wanted to construct a regular hexagon with the remaining 127 pieces. Starting with the border positions I got this solution:

3 colors, 92 two-sided pieces:

Constructions with different types of symmetry are possible.

We can remove one single colored hexagon and a hexagon of size 6 can be constructed with the border color of the removed piece.

4 colors, 700 one-sided pieces:

It's harder to work with so many pieces. In the triangle the lower part was covered first starting with the border positions. Pieces with many blue edges and at least one blue edge were prefered. For the upper part only few pieces with blue edges were left and a solution was found.

I noticed that 32^2-18^2=700 and wanted the construct a rhomb ring. Because the border is too long, I decided to take different colors for the outer and the inner border.

4 colors, 430 two-sided pieces:

There are 430*6/4=645 edges of same color. Therefore it isn't possible to get all edges matched. Instead of matching same colors we can look for two pairs of colors, which must touch (e.g. red and light red, blue and light blue). Now a construction is possible, if one color pair is used for the border and the colors of the pair alternate strictly. This way the construction can easily transfered to pieces with two pairs of male and female edges.

I-shaped, S-shaped and Z-shaped edges; 74 two-sided pieces:

The total number of straight edges in the set is odd. To construct a symmetric figure I used 73 pieces and left over one piece with one straight edge. Other pieces with an odd number of straight edges should be left over as well.

Straight, male and female edges; 130 one-sided pieces:

Since the number of pieces is the same as the number of pieces colored with three colors, I tried to solve the same figures already done with the colored pieces. In the program I had to change the matching rules to search for a solution. Afterwards I wrote a procedure to get SVG files for the constructions. The rectangle was already solved by Miroslav Vicher long ago and is shown at the PolyPages.

Straight, male and female edges; 92 two-sided pieces:

Because the shapes of the edges don't change, if they are turned upside down, the set has as many pieces as the set of hexagons colored with three colors and we can cover the same figures. The hexagon was already solved by Miroslav Vicher long ago and is shown at the PolyPages.

I-shaped, S-shaped, male and female edges; 700 one-sided pieces:

Instead of four colors matching oneselfs we have two colors matching oneselfs and two colors matching each other. Adjusting the matching rules in the program solution were constructed. For the endgame only few pieces with S-shaped edges are left in the upper part of the triangle. As with the colored pieces searching for the solution wasn't that fast due to the large number of pieces.

S-shaped, Z-shaped, male and female edges; 382 two-sided pieces:

If you turn over a piece with a S-shaped edge, the S-shape transforms into a Z-shape. Therefore the set is smaller than a set with two pairs of male and female edges. To get a solution I tried to use as many symmetric pieces as possible during the first stage of the search, because there are more options to place the other ones later on.

Male and female edges with square and triangle notches; 430 two-sided pieces:

The solution is exactly the one shown for two-sided hexagons with four colors, because in the colored version two pairs of colors match each other.