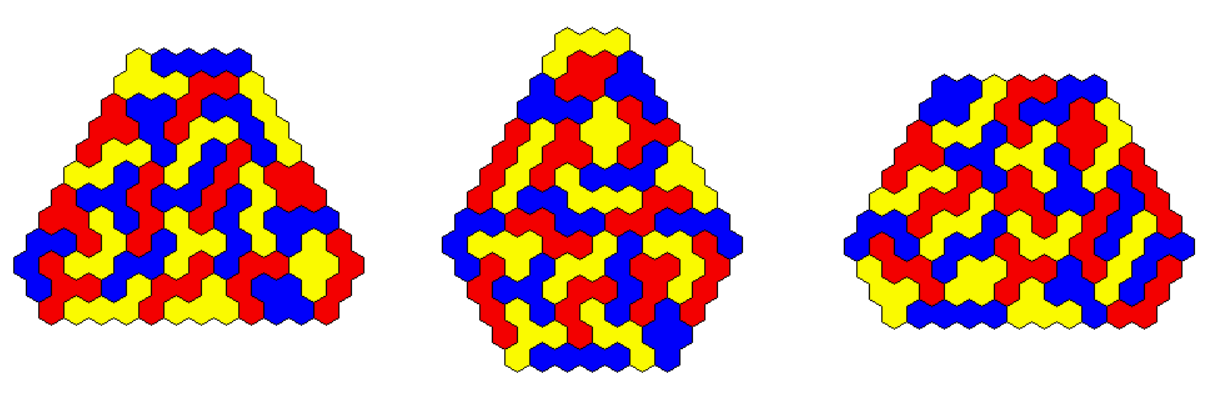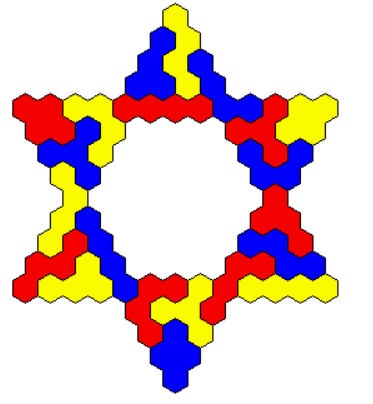
Three Sets of Two-sided Colored Tetrahexes

There are 3*7=21 pieces with a total area of 84. Since 6 is a divider of 84 we can get constructions unchanged under 60 degree rotation. In this case the center can't be covered. Here are three rings and one star.

Figures with rotational symmetry but with only three axes of symmetry or even no axis of symmetry are also given.

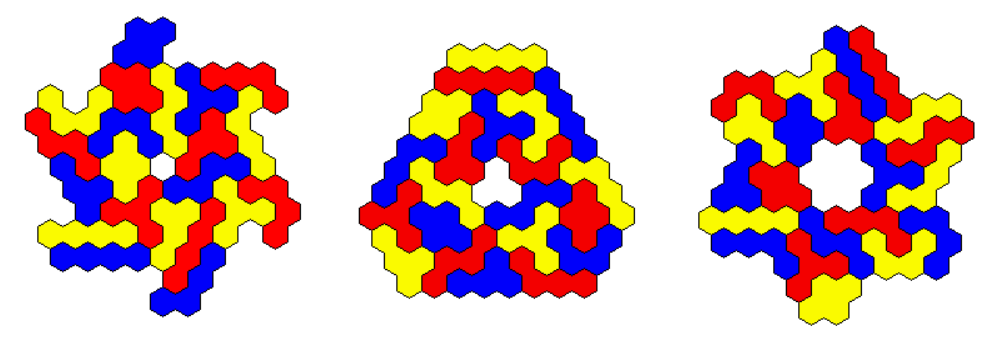
We can also construct a kind of oval or rectangle with two axes of symmetry.

Since 84 factorises very well we can make four different parallelograms.

Solving a(a+1)-b(b+1)=84*2 for 0 < b < a yields the dimensions for three trapezia.

Among a lot of convex 'hexagons' with an area of 84 I looked for figures with one axis of symmetry.

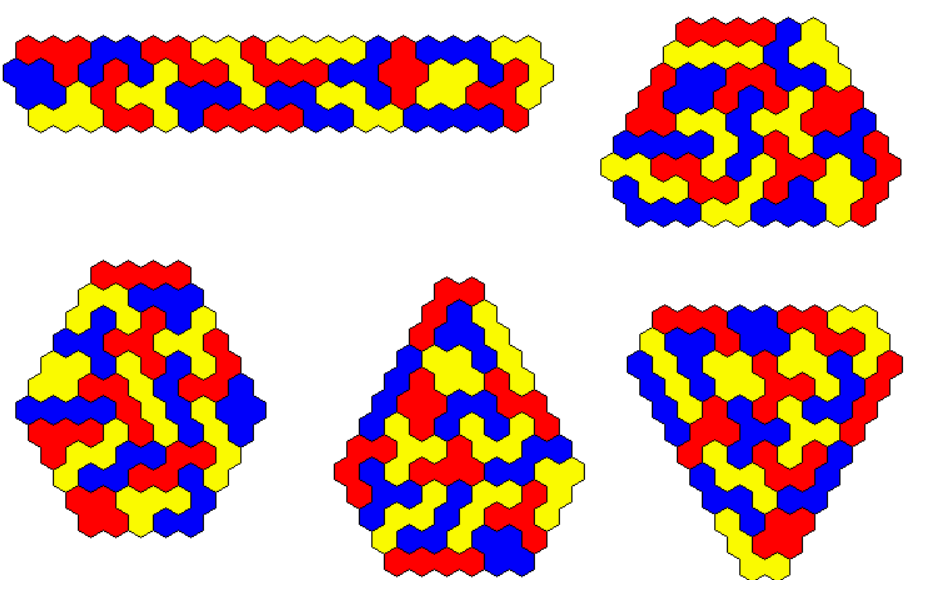
Three Sets of One-sided Colored Tetrahexes

We have 3*10=30 pieces with a total area of 120, just a perfect number for symmetric constructions. It seems to be better to print one-sided pieces with a 3d-printer because two-sided pieces slightly differ at the front and back side. Therefore I chose this set to get physical pieces. Here are two figures with hexagonal symmetry.

A kind of rectangle and a rhomb ring are patterns with two axes of symmetry.

I looked for hexagons with two axes of symmetry and inserted holes at the center to get a total area of 120.

Two trapezia can be made.

A pentagonal structure is also possible.

At last I solved some hexagons with no holes and one axis of symmetry.

Back

Home