

For five parallelograms of size 11x5 it seems to be impossible to get a solution, where the stripes in all parallelograms have the same direction; but with different directions it can be done.

For some shapes there are only two pieces with different directions of the stripes. Therefore we can't directly transfer a solution with one direction of the stripes into another one. A hexagonal structure with side lengthes of 4,38,4,4,38,4 hexagons and with two directions of the stripes is shown. You can get the third direction by reflection.

The same applies to a long rectangular structure. In the vertical version the rectangle is split into three parts.

Two other kind of rectangles are only shown with stripes in one direction. Solutions for the other two directions should be possible, too.


Since we have a total number of 275 hexagons and 275 mod 3 = 2, we can't get constructions without holes and with rotational symmetry of 60° or 120°. Instead I looked for some symmetric similar hole figures.


You can also fill the total area of 495 hexagons with 12 rows of size 22 plus 11 rows of size 21.

A kind of hexagon with one axis of symmetry is also given. To solve the whole pattern it was split into three parts. Do you see which part was filled at last?


Five hexagons of size 10 with a single hole are also possible, As with the last construction the hole can't be at the center.

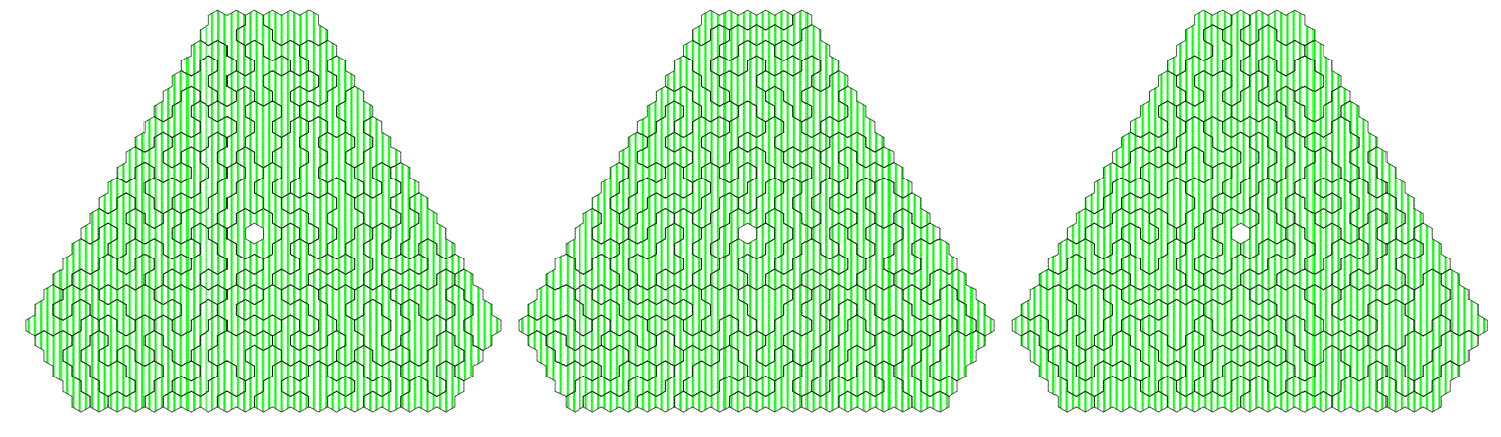
At last I constructed three congruent semiregular hexagons with a hole out of the center position.

We can also solve the following pattern two times with three heaxagons removed at one corner. You can join these solutions to get a hexagoanl ring.


Since 2592=3*864 and 864=10*45+9*46, I tried to fill three congruent kind of rectangles. For another integer solution of 864=a*b+(a-1)(b+1) with a=6 and b=66 a construction seems to be possible, too.
