Stacked Tetrominoes
The 18 stacked tetrominoes are a wonderful set for hand solvers. It's small enough to
get a lot of solutions within one or two quarters of an hour. If we choose the height of the
unit cell as 2/3 of its width we can turn the pieces around because edges with height*3 match
those with width*2. The fixed grid can be broken this way.
These are the pieces. Use the colors to identify the pieces in the following constructions.

Here are five boxes with all pieces aligned to the grid. But let's look for other ones. The I-tetromino doesn't fit into a
2x2x18 box if horizontally placed, but we can turn 3 layers with thickness 2/3 around to get
a column with width 2. This way three additional boxes are possible.

If you get bored with plain faces try these prisms with jagged cross sections.

Rings with a vertical hole and frames with a horizontal hole are possible, too.

If you want to display the pieces you might choose the following figures.

If the size of an unit cell is 1x1x2/3, a cube of size 2 can be made from 12 cells. Using all
pieces it should be possible to replicate all hexacubes i.e. 166 tasks. Fortunately with 3 dicubes,
3 pairs of tricubes, two combinations of a dicube with a tetracube and only one special hexacube all
problems can be solved.
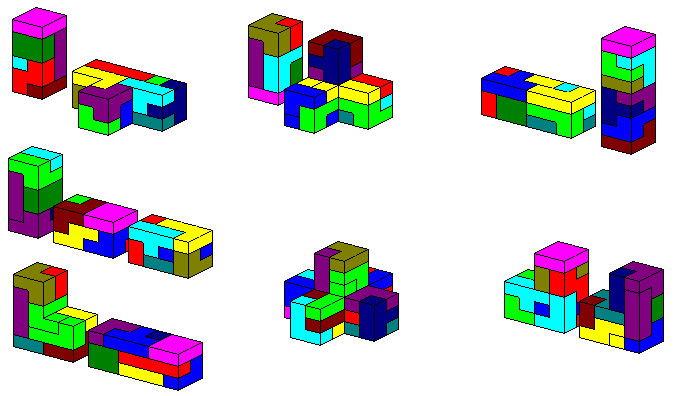
The pieces are easily cut and glued and it's a special challenge to
find construction with some parts hanging over. I think it's rather
difficult to let the computer find such a solution. The gate is made from the
three boxes described above.


At last there are two figures you can't get. The number of unit cells in the even layers 0,2,4,..
must be even. Translating a piece up or down or turning it upside down doesn't change this property.
But the house doesn't match this condition. For the open box the condition is true but a construction
isn't possible either.

Index
Home









