Pentaboxes
Here are the 147 pieces.

With 5*147=3*5*7*7 we can look for a 5*7*21 box where all edges are different. Using a unit cell
of size 4.2*3*1 the 5*7*21 box will be a perfect cube of size 21. I found this construction in December 2001.

In 2003 I had another look at the pieces and tried to make multiple constructions with the set.
With three congruent 5x7x7 boxes you can get the "cube" as well and also
the other possible 15x7x7 box. (show layers)

It's more difficult to find the three congrunet stairs but I like this construction very much.
(show layers)

Even seven congruent figures are possible. The rectangular towers with missing corners in the cross section
are an example. (show layers)
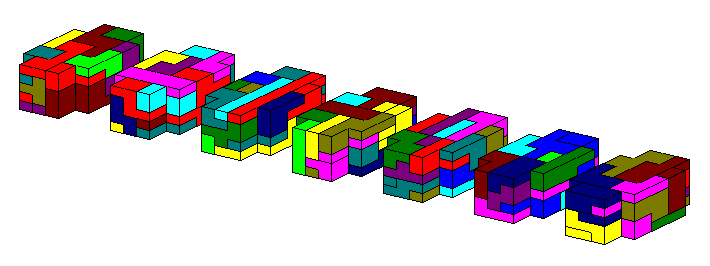
The seven stairs can also be combined to get some other constructions. (show layers)

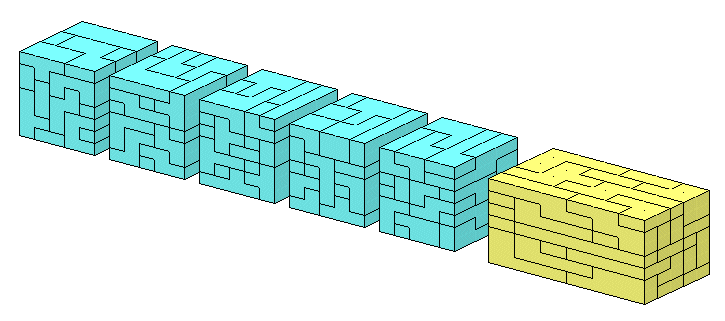
You can also get five 3x5x7 boxes and one 6x5x7 box. In the pictures the last box is turned
around.
Using a basic box of size 3.5 x 2.1 x 1.5 the resulting constructions are five cubes and one dicube which can be combined to make replicas of all heptacubes.
(show layers)
At last you can see the cube with wooden pieces:

Index
Home








