Tetraboxes
Here are the 32 pieces.

Two 4x4x4 boxes can be constructed and if we combine these two boxes
we get the 4x4x8, the 4x8x4 and the 8x4x4 boxes. No other ones are
possible because the length of each edge must not be smaller than 4.

Instead of the two congruent boxes we can also make two pairs of congruent
boxes which allow for a lot of various combinations.

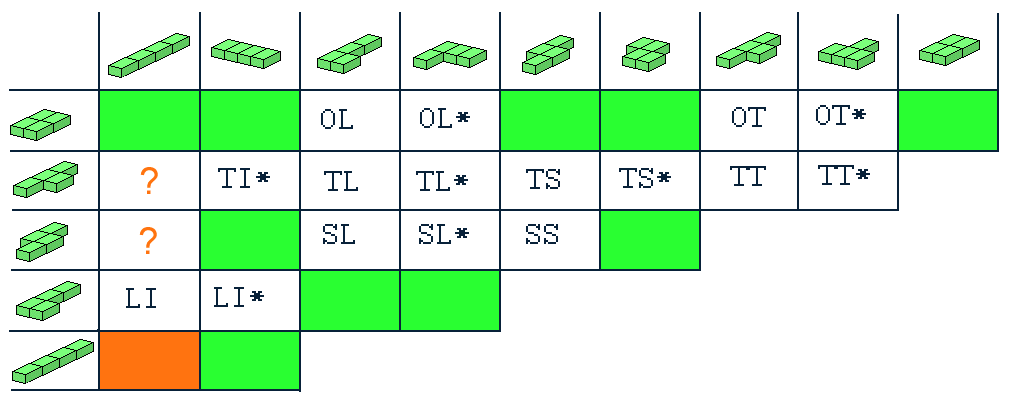
The two 4x4x4 boxes are prisms of height 4 with a flat tetrarectangle as
cross-section. Therefore we can ask for constructions with the other flat tetrarectangles as
cross-sections. The table shows the possible combinations. The red field isn't possible, the green
fields can be derived from the previous solution, for the cases with the question mark
I didn't find a solution and for the remaining cases the layers are provided.
(with T-tetro and without T-tetro).
If a solution for XY* is given you can easily get the solution for YX* by replacing all pieces P
by P* and vice versa.
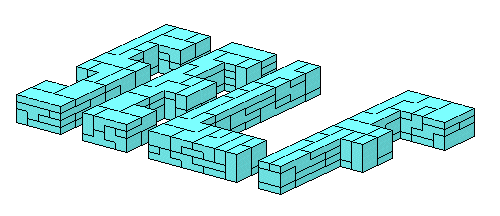
The prisms with tetrarectangles as cross-section can be used to get prisms with octarectangles as cross-sections
but for some of these figures special constructions are needed as for the 'E' in the following picture.
Only for the two straight octarectangles there is no solution. But if the side to side ratio of the elementary
rectangles is 2 to 3 we can use a trick and get a model of one straight piece.

If we start with a 6x6 cross-section and remove four single rectangles we get holey
prisms of height 4. Some symmetric examples are shown and it's also possible to shift the holes to the borders.
The layers are here.

At last you can see three jagged constructions and one cross tower.
The layers are here.
I tried to split the
bottom right figure into two triangles but unfortunately I haven't got a solution until now.
Maybe it's impossible.

Index
Home








