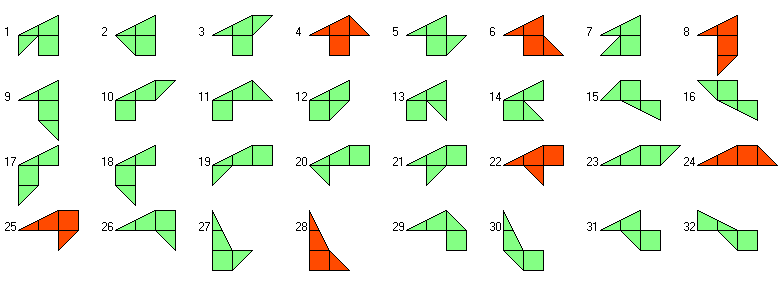In 2001 Roel Huisman suggested a set of polyforms made up of a square, a sliced square (tan) and a sliced domino (dom).
There are 32 two-sided pieces and some constructions with this set are shown on
Roel's site.
and on The Poly Pages. Since all pieces are
asymmetric we get 64 pieces if we consider the one-sided pieces. This set can cover an area of size 160 and a lot of new constructions
are shown here. But first let's have a look at the original set.
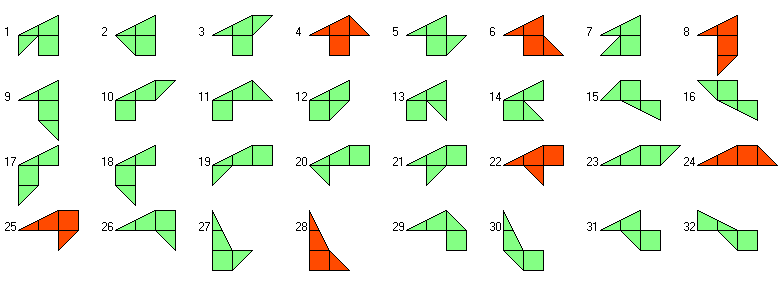
1. Constructions with the two-sided pieces
The first problem in 2001 was a dissection of a 5x16 rectangle. Handsolving is very hard with this set and therefore I modified an existing program
to work with sliced pieces. This way many constructions of rectangles, parallelograms, trapezia and multiple shapes were found.
On the 6th of Februrary in 2001, I started to make quadruplications of the pentominoes and the last replica
of the X-pento was found on the 26th of March in 2001.
Now, in 2006 with computers much faster and programs slightly better all twelve replicas were found in about one an hour.
Especially splitting the X in two fixed parts saved much computer time.

I had another look at convex polygons with two lines of symmetry. We can get polygons with 4, 6, 8, 10 or 12 corners
and even the square of size 4sqrt(5) which was hard to solve five years ago doesn't take much time now. The dodecagon with
rotational symmetry seems to be the polygon with minimum perimeter.

There are some figures with pentomino shaped holes at roel's site and I tried to solve all cases.

It's also possible to make 10x10
squares with pentomino shaped parts uncovered. Unfortunately the uncovered parts cannot be totally enclosed .

Beside the 9x9 square with an 1x1 hole, which I found in 2001, a new similar hole figure with a tilted square
is shown. Even now this was rather hard to find.

2. Constructions with the one-sided pieces
Since there are only asymmetric pieces in the two-sided set, the one-sided set is suitable to get
symmetric constructions. Try a pattern with the two-sided set, mirror it and a symmetric pattern is found.
Four rings and two other shapes are shown with one ring breaking the grid structure.

Those constructions are no real challenge since essentially the two-sided set is used. But if you are looking for eightfold
replicas of the pieces which aren't symmetric you have to work with the one-sided set with twice as many pieces, which
can't be flipped reducing their tilability. Six pieces and their mirror pieces cannot be replicated at all.They are marked
red in the picture of the set. To fill their 30°angle and their 45° angle you need two copies of piece number 24 and thus
a construction fails. Two replicas are shown the remaining ones are here . As you can see parts of the construction are identical
in different replicas.
After this work was finished a new problem arose. Is it possible to make fourfold replicas of the decominoes?
3611 out of 4655 decominoes are a combination of two pentominoes. If you can replicate each combination of any two pentominoes a lot of the problem is solved.
Six cases are considered.
a) Pentomino and its Mirror Piece
For these combinations the replica of the decomino is given by the replica of a single pentomino with the two-sided set and the reflected construction.

b) Identical Pentominoes
Only the asymmetric pieces must be regarded. For symmetric pieces the identical piece can be seen as its mirror piece and case a) applies. One solution is shown all
six solutions are here .

c) Two Different Symmetric Pentominoes
Since there are six symmetric pieces we have 6*5/2 = 15 problems. The solution shown uses the two-side set for half the construction. Unfortunately
this approach isn't possible for all combinations. All solutions are here .

d) Symmetric Pentomino plus Asymmetric Pentomino
With six symmetric and six asymmetric pieces 36 problems are to be solved. For the mirrored asymmetric pieces
the whole constructions must be mirrored. The set of solutions is divided in
combinations with YNL and with ZPF .

e) Two Different Asymmetric Pentominoes Both Unmirrored
There are 6*5/2 = 15 combinations. If both pentominoes are mirrored the given solution must also be mirrored.
All solutions are here .
f) Two Different Asymmetric Pentominoes With One Piece Mirrored
As in case e) we only have 6*5/2 = 15 problems, because the other piece will be mirrored, if the whole construction is reflected.
All solutions are here .

At last I tried to replicate all symmetric decominoes.

As the picture shows many symmetric decominoes are
a combination of two pentominoes. For the remaining
pieces I split the whole piece in one or two pairs of symmetric parts and solved half the shape with
the two-sided set. Two examples are shown, all solutions are here ..

This strategy failed for the red colored pieces and a special search for
each shape was neccessary. Using some parts of existing constructions reduced the time needed.
Two examples are shown, all solutions are here .

Don't know when I feel like solving the missing 1006 problems.
To display some of the constructions I sawed the pieces, attached little magnets on
the backside and put the pieced on an iron board.

Home