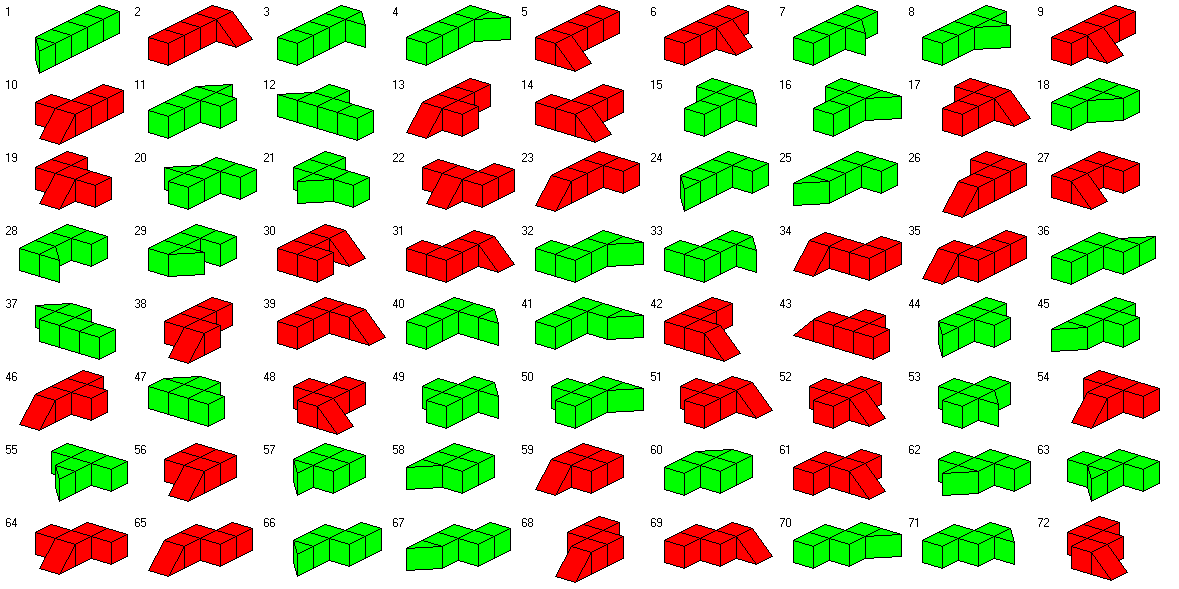
Solid 4.5ominoes
2019/08/17

Take a solid tetromino of unit thickness and attach a unit cube to a vertical square face of it.
After this we remove half of the attached cube by a single diagonal cut,
so that the other
half of the cube remains attached to the tetromino. If the cut is vertical we can get 38
different pieces which are prisms. Otherwise 34 pieces with kind of ramps are possible.
Here are all 72 pieces with a total
volume of 324 unit cubes. The prism pieces are green colored and the other ones are red colored.
Because 324 factorises very well a lot of constructions are possible.
To get physical pieces I printed them with a unit length of 15mm. You can get obj files for printing at
thingiverse.

What can be done with these pieces? I constructed
rectangles,
boxes,
open boxes,
rings or tubes and
spirals.
Click the pictures to get numbered solutions. A white mark at a number indicates a slope going
up from this piece.
Rectangles
Rectangles of size 4x81, 6x54, 9x36, 12x27 and 18x18 can be constructed by the following sets of equal rectangles.
Three rectangles 4x27

Four rectangles 9x9

Six rectangles 6x9. Each rectangle might be a puzzle for solving by hand.

The 9x36 rectangle can also be made by a 19x9 rectangle using only prism pieces and a 17x9 rectangle
using the other ones.

Boxes
There are many boxes with at least one edge of size 2 or larger: 2x9x18, 2x6x27, 2x3x54, 3x3x36, 3x6x18,
3x9x12 and 6x6x9. All boxes but one can be constructed using the multiple rectangle solutions or the
following multiple box solutions.
Three boxes 3x3x12

Four boxes 3x3x9

The 2x3x54 box was rather diffcult to get, because of the small cross section. At last a dissection
into a 2x3x30 box and a 2x3x24 box worked. First a 2x3x25 box was solved 1000 times, and it was determined
how often each piece from the set was used. Then the large box was solved using as many pieces as possible
with little frequencies and no pieces with high frequencies. With the remaining good pieces the small
box could be completed.

Open Boxes
I constructed two open boxes with wall thickness of one unit length. To reduce the depth of the search tree
I dissected the whole figure into three parts and solved each part separately.
Open box 25x6x4

Open box 25x8x3

Rings or Tubes
The ring with a cross section of 10x10-8x8 and height 9 can be made using the four rectangles of size 9x9.
The tube with a cross section of 4x4-2x2 and height 27 can be solved but a physical construction would
crash. Therefore I combined the two parts of the construction to get a U-profile of length 27.

For the ring with a rectangular cross section of 16x13-14x11 and height 6 a physical construction is
possible.

Another ring with a cross section of 12x12-6x6 and height 3 can easily derived from the
four boxes of size 3x3x9 and is shown at the title.
Spirals
Because the solution for the 2x3x54 box was rather hard to get, I thought a zigzag construction with
a 2x3 cross section might be easier to solve, and actually I found this solution:

Spirals with the same cross section are also possible.


Home

















