Two-sided Rounded Tetrahexes
Here is the set of 52 rounded tetrahexes with a total area of 208.
The SVG-file of these pieces is here.

A semiregular hexagon made with these
pieces is shown in the title and is an example of a figure with triangle symmetry.
Figures with one or two axes of symmtry ar shown below.



Parallelograms are also possible.
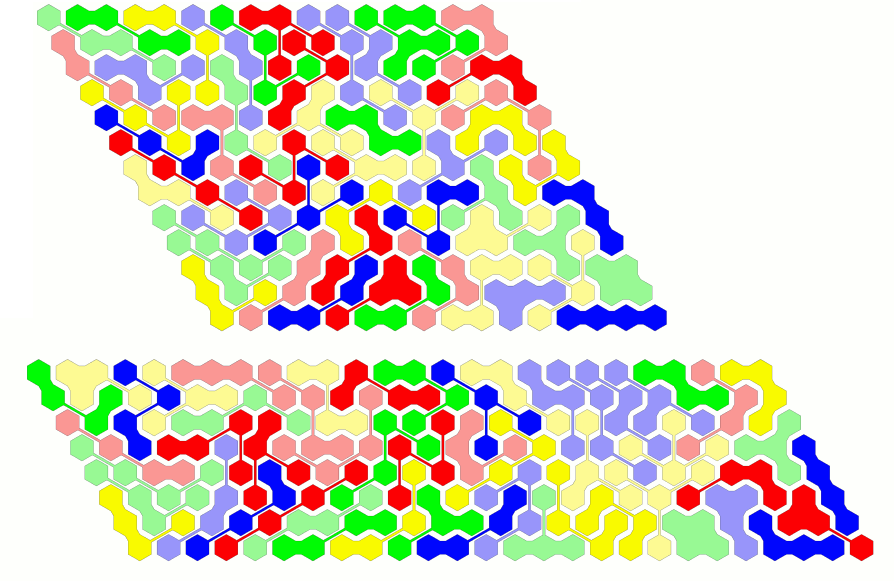
For jagged rectangles we need an area of size A=N*L+(N-1)*(L+1) or A=N*L+(N-1)*(L-1).
There are some integer solutions for A=208/2=104. Therefore I tried to construct pairs of those rectangles.

At least I wanted to get four congruent symmetric figures. The solution for the berry was found rather fast,
because the border is more jagged than that of the rectangle.


One-sided Rounded Tetrahexes
Here is the set of 89 one-sided rounded tetrahexes with a total area of 356.

Since 356 mod 3 = 2 and 356 mod 6 =2 it's
impossible to cover figures with hexagon or triangle symmetry. But we can construct hexagons with 180 degree rotational
symmetry.

A hexagonal ring with two axes of symmetry is also possible.

Since 356=256+100 I also looked for two rhombs of size 16 and 10.
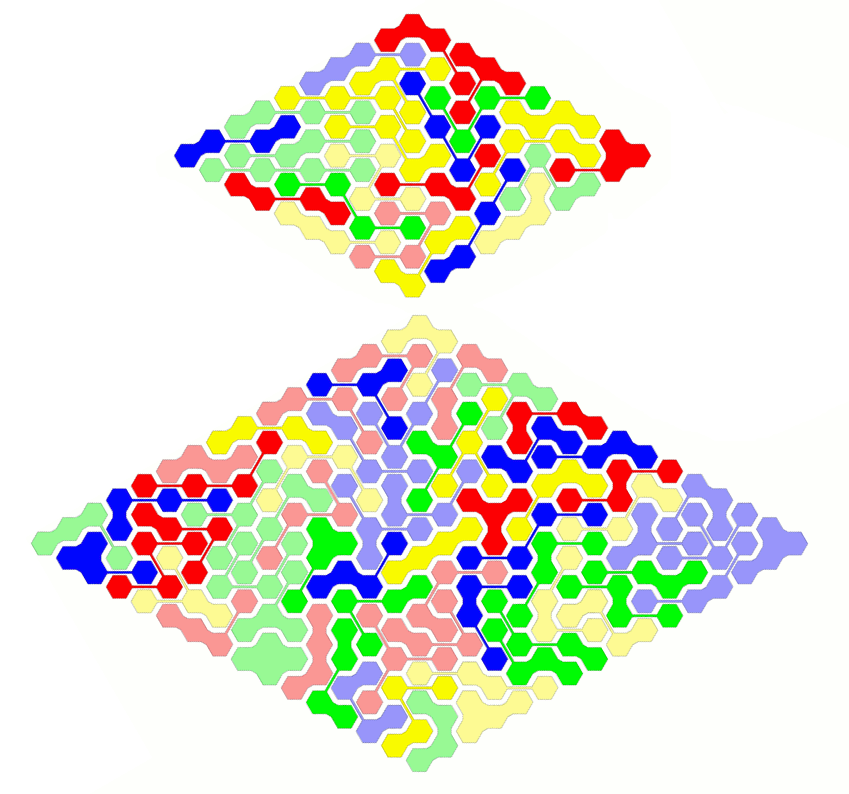
I found four different kind of rectangles: 5*40+4*39, 40*5+39*4, 16*11+15*12 and 12*15+11*16.

A construction with the real pieces confirmed the computer solution.

Back
Home














