All Except Same Colored Rhombs
If all color combinations are allowed and the number of colors is odd we get an odd number of
pieces. These sets aren't suitable for coverings and I discarded pieces with same colored sides to
get an even number of pieces for all numbers of colors.
3 Colors, 42 Pieces
Since all 28 terarhons have 4*10+2 faces or less this is a perfect set to cover those figures. A kind of tripod is shown.

Click the numbers to see other tetrarhons with 42 faces (yellow colored), 40 faces (green colored),
38 faces (blue colored), 36 faces (pink colored).
4 Colors, 132 Pieces
Chains of 13 rhons have 13*10+2=132 faces. Only the straigth one is shown.

With more connected faces a construction with 16 rhons is also possible.
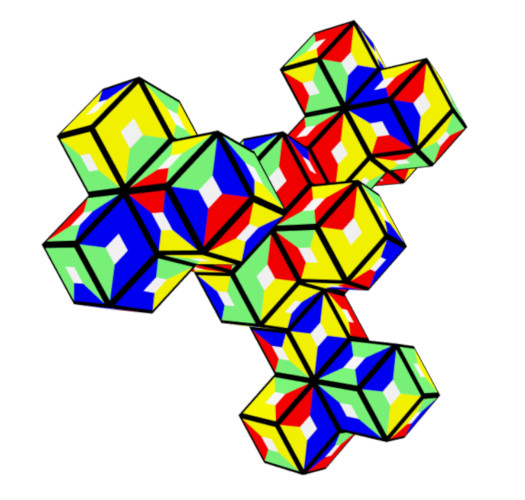
5 Colors, 320 Pieces
A pentagonal arrangement of rhons in the hexagonal grid can be made.
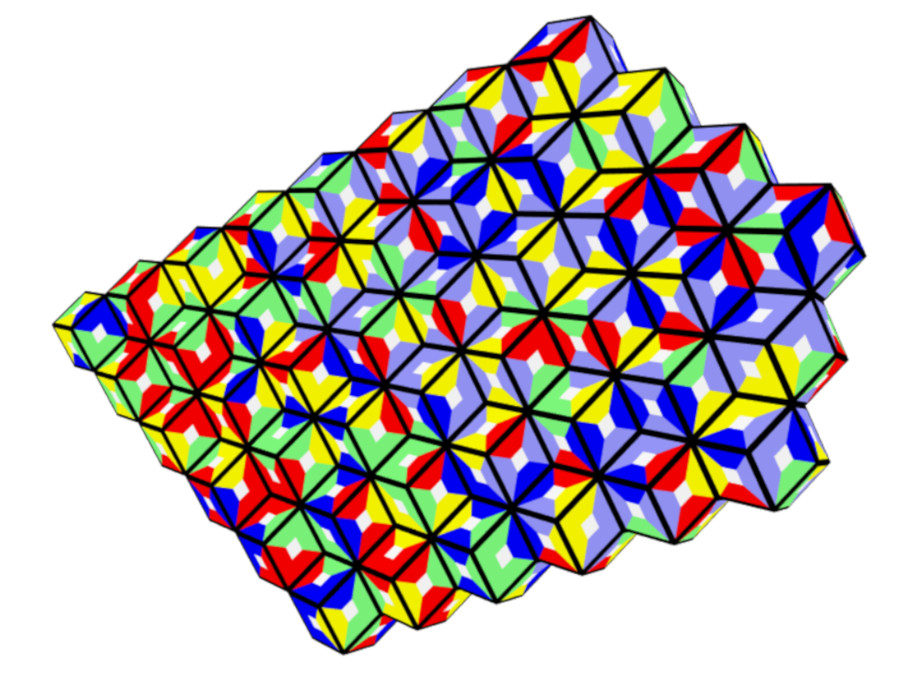
6 Colors, 660 Pieces
I solved a hexagonal structure of rhons with all pieces.

Figures like a tetrahedron made from rhons have a surface area of n*(n+1)/2*4*3 faces. For n=10 we have
660 faces and we can get a covering of this kind of tetrahedron.

Back
Home






