
What about a single rhon? Since a single rhon has 12 faces the 12 different rhombs using 4 colors might cover it. But this is impossibe. 12*4/4/2=6 edges of same color must be distributed so that they aren't sides of one rhomb and this can't be done. Therefore I looked for constructions with n>4 colors.

The hexagonal ring and the hexagon made from six rhons can be covered by the set. A physical construction of the ring is shown in the title.


Most hexarhons have 6*10+2=62 faces, but there are also some other hexarhons with two additional faces, which are connected, giving a surface of 60 faces. Two pieces in the orthogonal grid, looking like hexominoes, are shown.
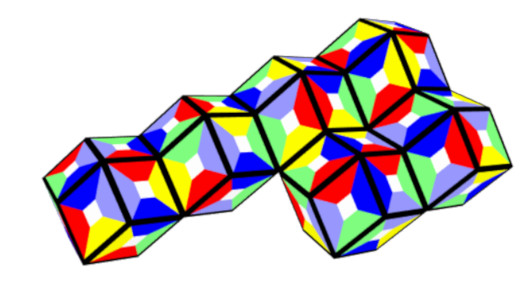

Here are two non planar polyrhons with 60 faces.
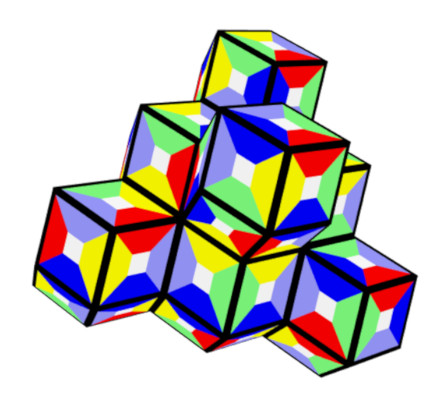
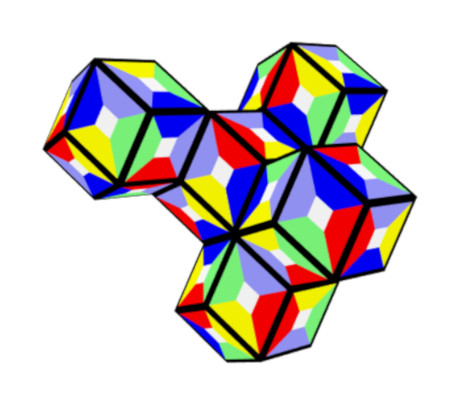
Five single rhons with no touching faces can also be covered.

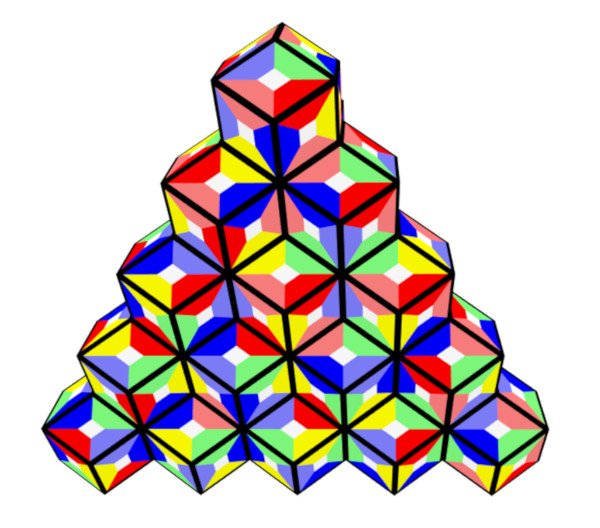
Chains of 18 rhons have 18*10+2=182 faces, but if the chain is closed like a ring we get only 180 faces.




With better algorithms, faster computers and more time larger constructions might be possible, too.
| 1 | 2 | 3 | k | |||||
|---|---|---|---|---|---|---|---|---|
| Colors | 4 | 7 | 8 | 11 | 12 | 15 | 4k+1 | 4k+3 |
| Pieces | 12 | 420 | 840 | 3960 | 5940 | 16380 | (4k+1)!/(4k-3)!/2 | (4k+3)!/(4k-1)!/2 |
| Size of Square | 1 | 7 | 10 | 22 | 27 | 45 | 4k^2-3k | 4k^2+3k |