Rhombs with All Color Combinations Allowed
If n colors are given, the number of pieces is (n^4 + n^2)/2. If n is odd the number of pieces is
also odd and sets with an odd number of pieces can't be used to cover polyrhons, because the number
of faces for these figures is always even. We have 12*i-2*j faces for i rhons with j connected faces.
Since chains of i rhons have 12*i-2(i-1) = 10*i+2 faces, the sets with 136 or 666 can't be used to cover
such chains. Therefore I looked for kind of two dimensional layers in the hexagonal or orthogonal grid
structure.
4 Colors, 136 Pieces
I constructed a rectangle and two other symmetric figures. In the orthogonal grid we have corners
of order 4 at the top of the rhons, and in the hexagonal grid the corners at the top are of order 3.
Click the pictures to turn the constructions around.
The 5x3 rectangle

3 Stripes in the orthogoanl grid

3 Stripes in the hexagonal grid

6 Colors, 666 Pieces
How to get hexagonal polyrhons with 666 faces? A triangular figure of rhons consists of k(k+1)/2 rhons
and f(k)=k(k+1)/2*6 + 6k faces. Since f(k)=666 has no integer solutions I looked for hexagonal figures,
which can be made by subtracting three small triangles from a large one. This way we get
f(x)-f(a)-f(b)-f(c)+4(a+b+c) faces, and the sides of the hexagon are x-a-b, a+1, x-b-c, b+1, x-c-a, c+1.
I covered three of such figures with the 666 rhombs. At first an order to cover the rhons and their
faces must be determined. Partial solutions with 660 pieces popped up very fast but
a complete solution wasn't found. Therefore I split the search algorithm into two stages. Among
the first 310 placed rhombs at least one side had to be light red colored. After a partial of 600 was reached
with this condition a part of the partial was used to complete the whole construction.
Click the pictures to turn the constructions around.
Hexagon 2-5-14-5-2-17
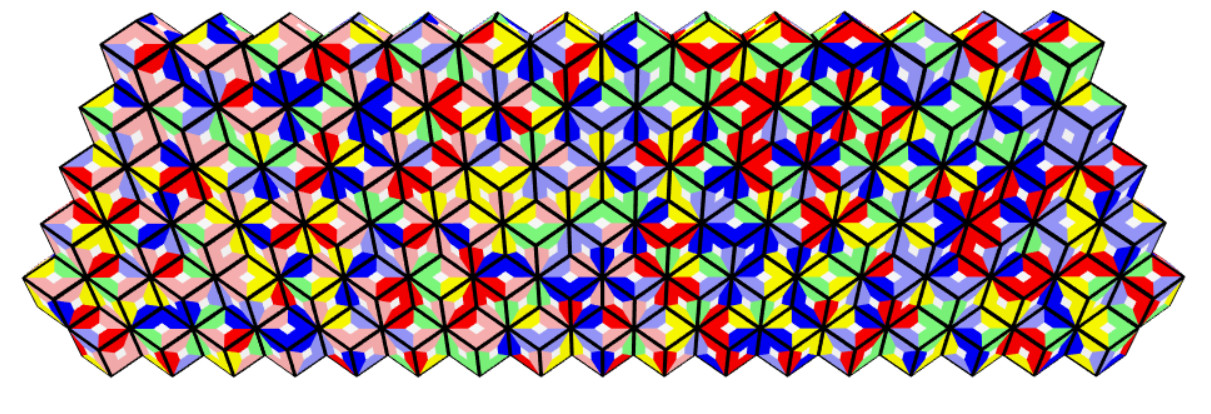
Heaxagon 6-8-3-11-3-8

Heaxagon 5-7-5-10-2-10

Back
Home






