Pseudo-Polycubes
2007/01/06

Usually polycubes are constructed by connecting cubes face by face.
For the pseudo-polycubes connections by edge or corner are additionally allowed.
Solomon W. Golomb introduced this kind of polycubes in his book about polyominoes. I wanted to make a physical representation
of these pieces but it seemed to be hard to get a sturdy connection between two corners. Therefore I discarded the
pieces connected at corners and looked for sets where only faces or edges are connected. In this case the cubes were easily joined
with two crossing stripes of transparent plastics.
If pieces and their mirror pieces are counted as distinct pieces, I get the following table:
| Number of Cubes |
Allowed Connections |
|
Only Faces (2-dim) | Only Faces (3-dim) | Faces and Edges (2-dim) | Faces and Edges (3-dim) | Faces, Edges and Corners |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 | 3 |
| 3 | 2 | 2 | 5 | 9 | 16 |
| 4 | 5 | 8 | 22 | 88 | 246 |
| 5 | 12 | 29 | 94 | 1103 | 4866 |
| 6 | 35 | 166 | 524 | 17570 | 115520 |
| 7 | 108 | 1023 | 3031 | 295506 | |
For some pieces it is possible to remove one connection between two edges without the piece falling apart.
Should these pieces with different connections be counted as distinct? In some cases a missing
connection can make a construction possible in other cases there is no influence.
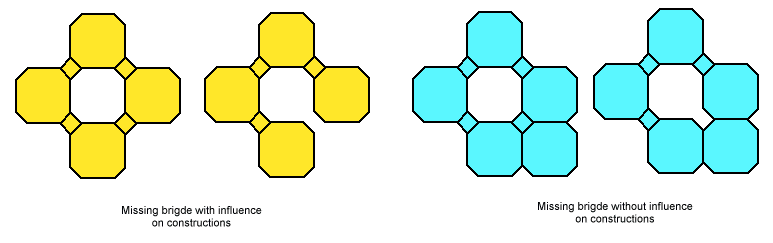
Therefore I decided
to assume a connection or bridge between all adjacent edges and in the constructions bridges aren't allowed to
overlap. This is a significant difference to the pseudo-pentominoes introduced in the pentomino section of my site.
Other 2-dimensional polyforms with bridges are analyzed by Bernd Karl Rennhak at his site.
Unfortunately the 88 pseudo-polycubes of order 4 have a parity problem and you cannot make a box with these pieces.
To get some more constructions I had a look at sets consisting of order 1 through n pseudo-polycubes. Click the numbers to see some of them.
One box is shown below.
| Number of Cubes |
Allowed Connections |
|
Faces and Edges (2-dim) | Faces and Edges (3-dim) |
| Pieces | Total Volume | Pieces | Total Volume |
| 1 | 1 | 1 | 1 | 1 |
| 1..2 | 3 | 5 | 3 | 5 |
| 1..3 | 8 | 20 | 12 | 32 |
| 1..4 | 30 | 108 | 100 | 384 |
| 1..5 | 124 | 460 | 1203 | 5899 |
| 1..6 | 648 | 3604 | 18773 | 111319 |
| 1..7 | 3679 | 24821 | 314279 | 2179861 |

Home



