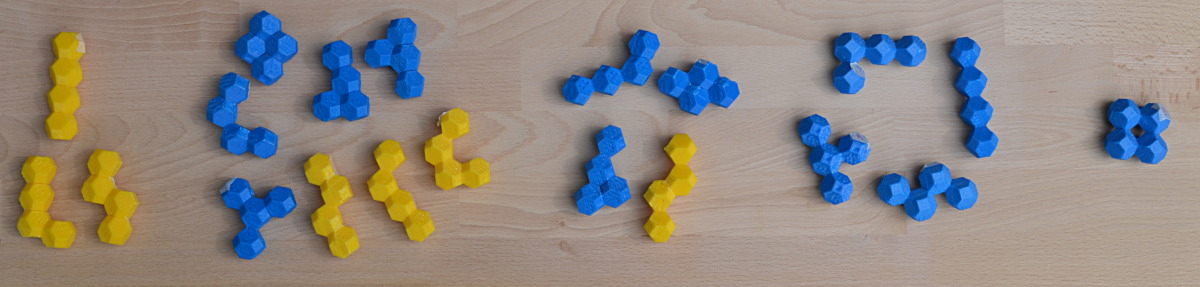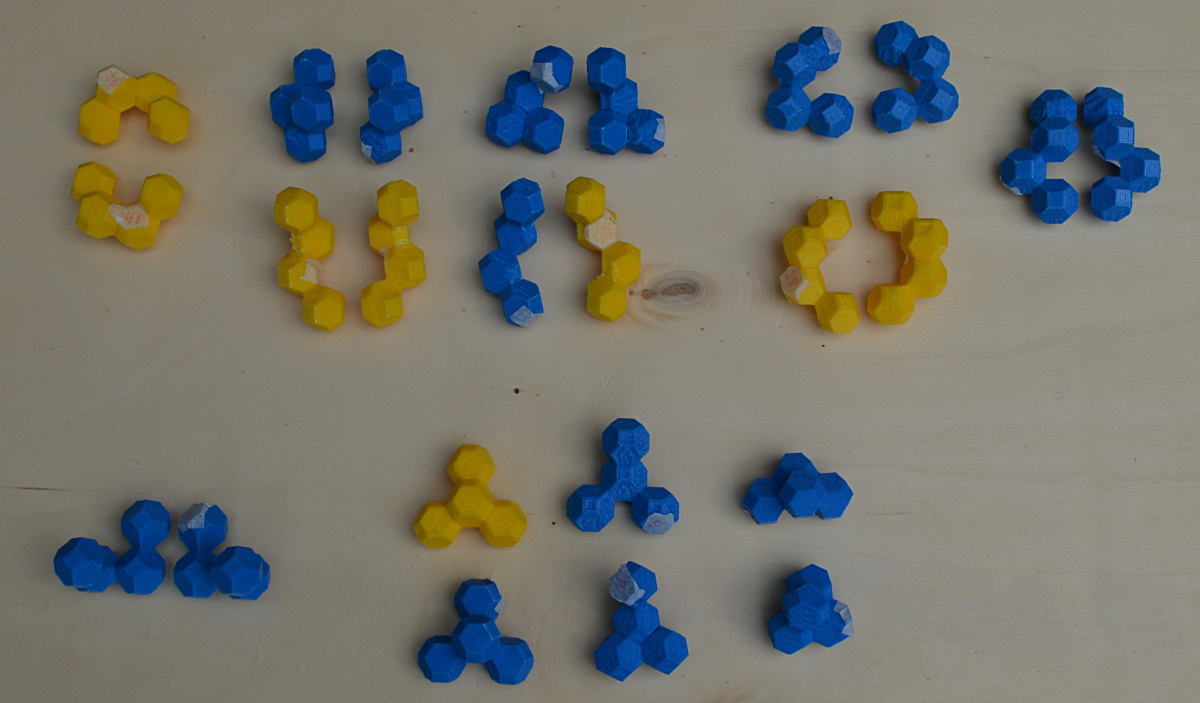Tetratrocs
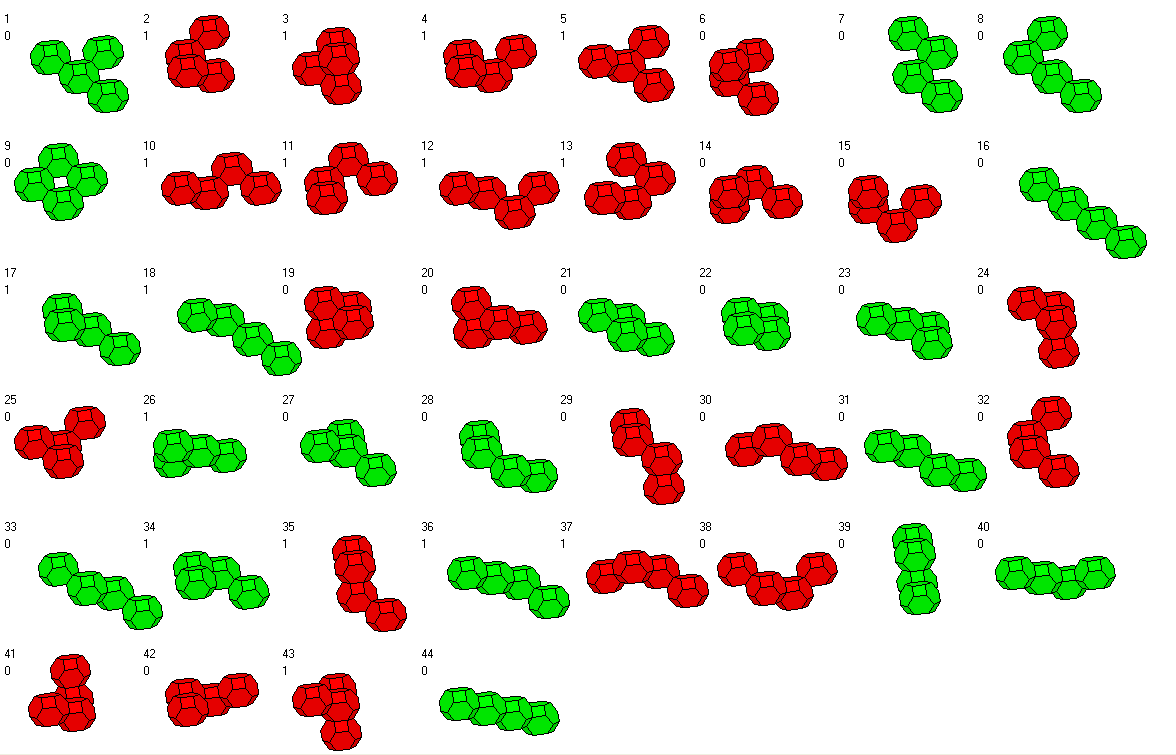
These are the 44 tetratrocs with a total volume of 176. The 20 planar pieces are colored green and the 24 non-planar
ones are colored red. The numbering was given by the generating program and is used in the layer pictures.
The additional 0 or 1 indicates an even or odd piece, respectively. What does that mean? Let's use a checkerboard coloring
of the pieces with two colors. If two truncated octahedrons are joined at square faces they get the same color,
if they are joined at hexagonal faces they get different colors. A pieces is even if the number of same
colored parts is even. Fortunately the number of all odd pieces is even and there are no problems
with symmetric constructions.
I started printing the pieces with blue PLA but the quality was rather bad. Then I ran out of material and stopped printing.
Later on after adjusting printing parameters I tried to print the missing pieces with yellow ABS. This was slightly better
and now it was possible to assemble some constructions. Here are the planar and the non-planar printed pieces.
Non-planar mirror twins are placed together.
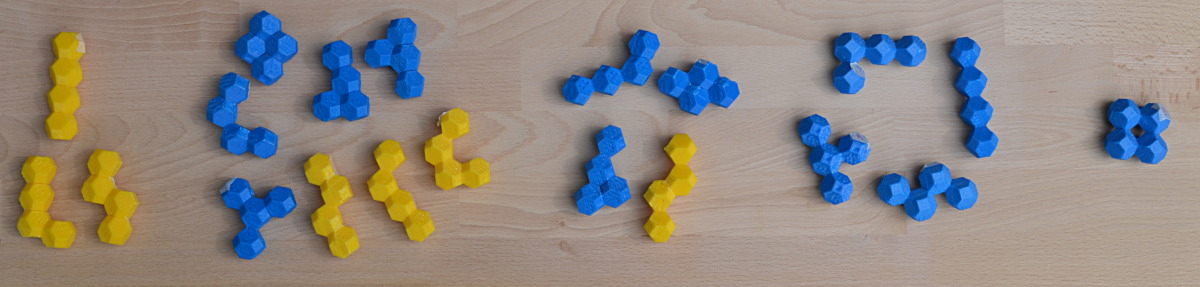
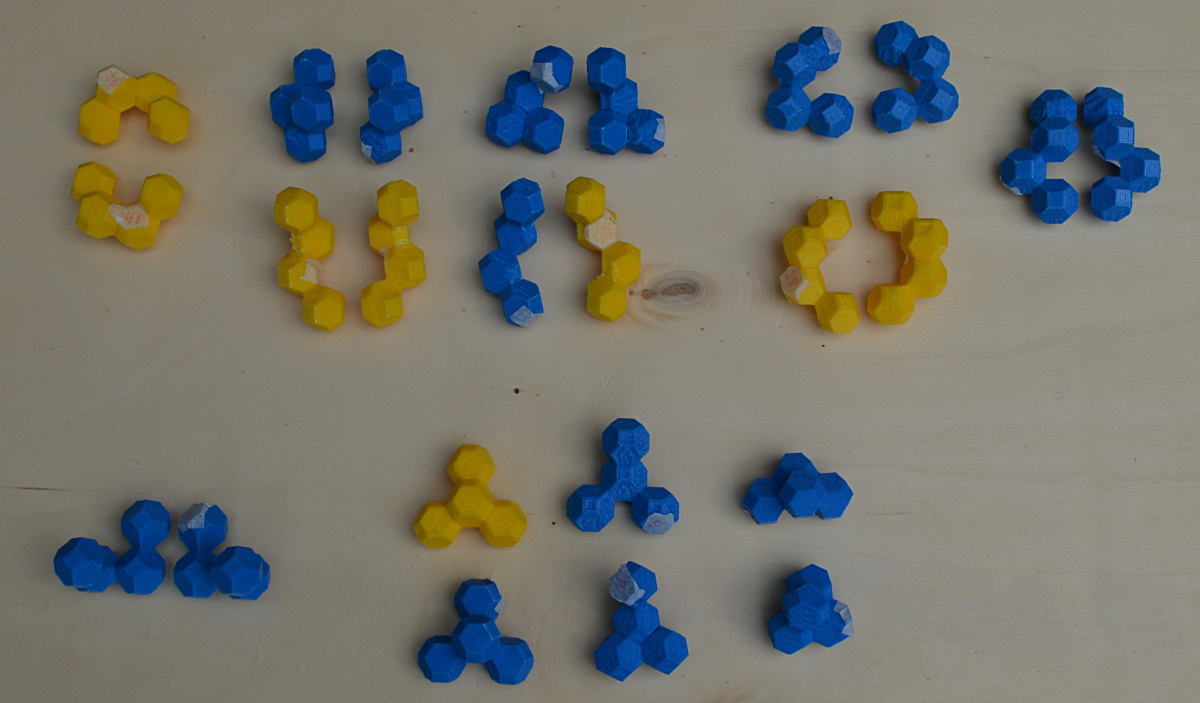
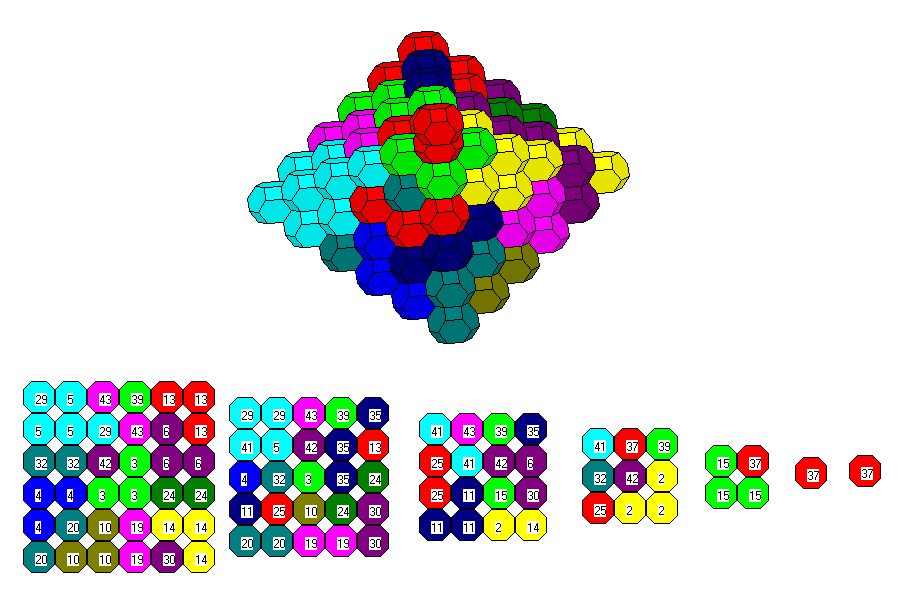
The box with three layers of size 8x5 and two layers of size 7x4 has three planes of symmetry. Click the
picture to see the layers.

A square pyramid of size 8 consists of 204 units, too many for the set. But we can remove 4*7=28 units
at the four edges getting a figure, which is symmetric under rotation of 90, 180 or 270 degrees
around the z-axis.

The 6x10 roof with a single truncated octahedron on top is symmetric under rotation of 180 degree.

Instead of a single figure you can also make a pair of constructions with the whole set.


To avoid problems with pieces wrapped around each other you can take the subset of 20 planar pieces.
Unfortunately the number of odd pieces among this subset is odd, so that symmetric figures with
volume 80 aren't possible to construct. Examples with volume 76 are shown.

Only 16 planar pieces fit the hexagonal grid but the number of odd pieces in this set is odd. Therefore
the shown figures consist of only 15 pieces.

Among the 24 non-planar pieces the number of odd pieces is odd, too. So an odd piece must be left over to
get a symmetric construction. Be aware! The computer solution isn't checked. The real construction may fail
because of the wrapping issue.
Back
Home