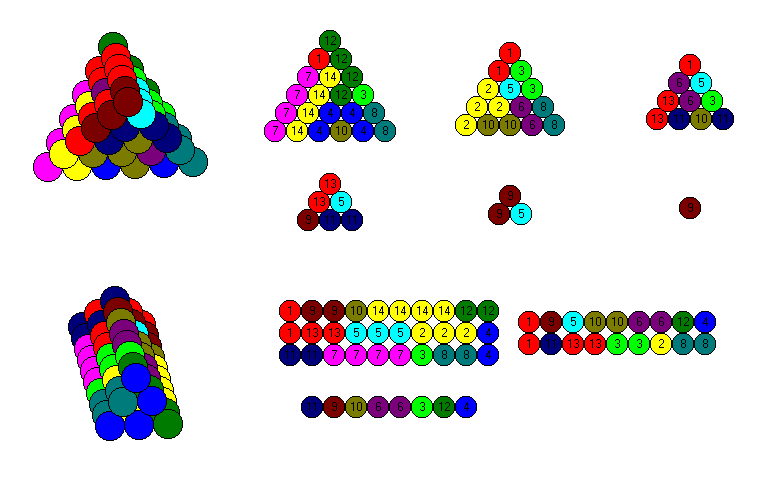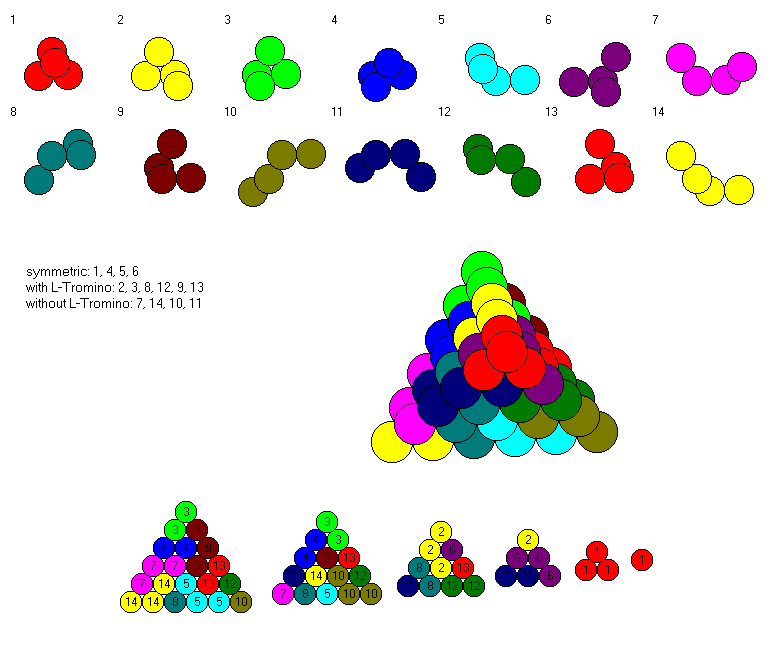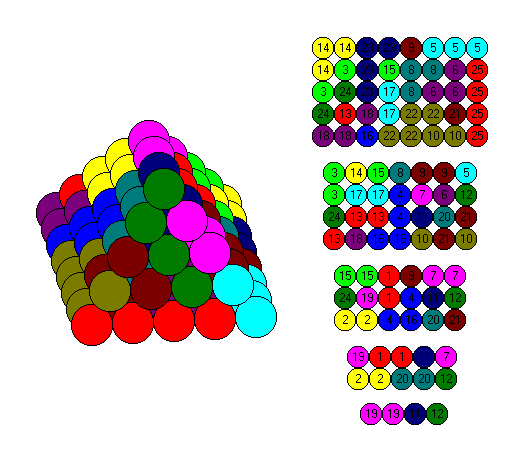Tetraspheres
There are only seven pieces which are planar in the hexagonal grid i.e. the seven tetrahexes. The set is very small and only one symmetric solid is shown.
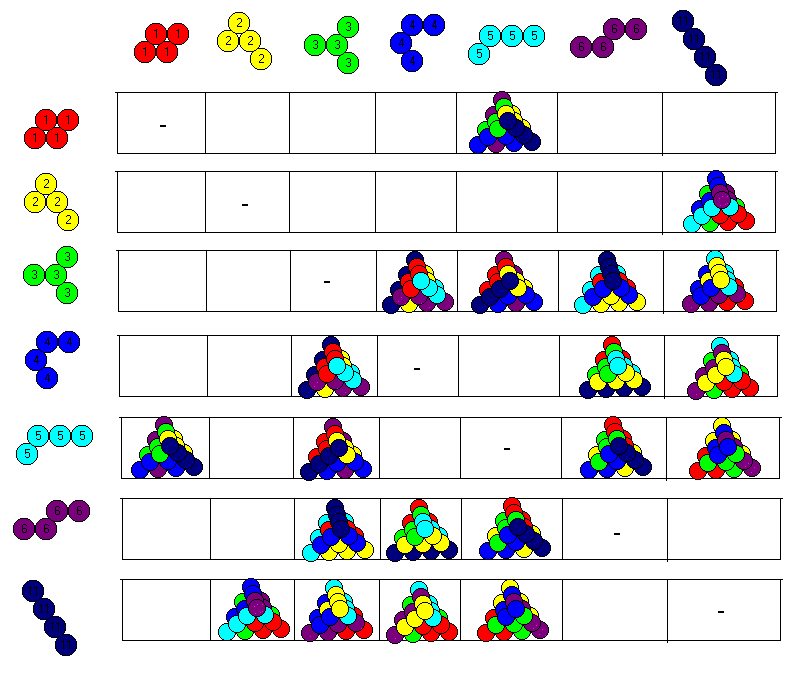
If we choose 5 out of 7 pieces, we can make a size 4 tetrahedron. The table shows the combinations of any two pieces, which can be omitted.
With two sets a 3x10 roof and a size 6 tetrahedron are possible to get.
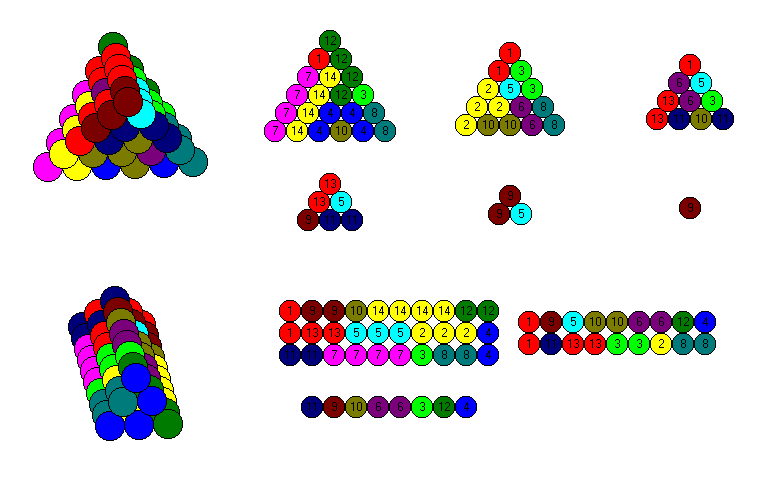
I made the pieces from marbels, which were glued together by an elastic glass adhesive.

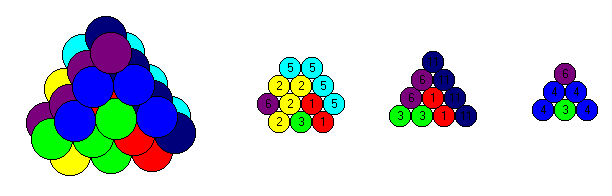
Here are the 11 planar tetraspheres with 6 pieces planar only in the hexagonal grid and 4 pieces planar only in the square grid and the straight piece in both grids. Perhaps you'd like to find a solution for a size 4 octahedron or a 3x8 roof by hand.
I made the pieces from table tennis balls glued together with a hot glue gun which gives a sturdy connection.

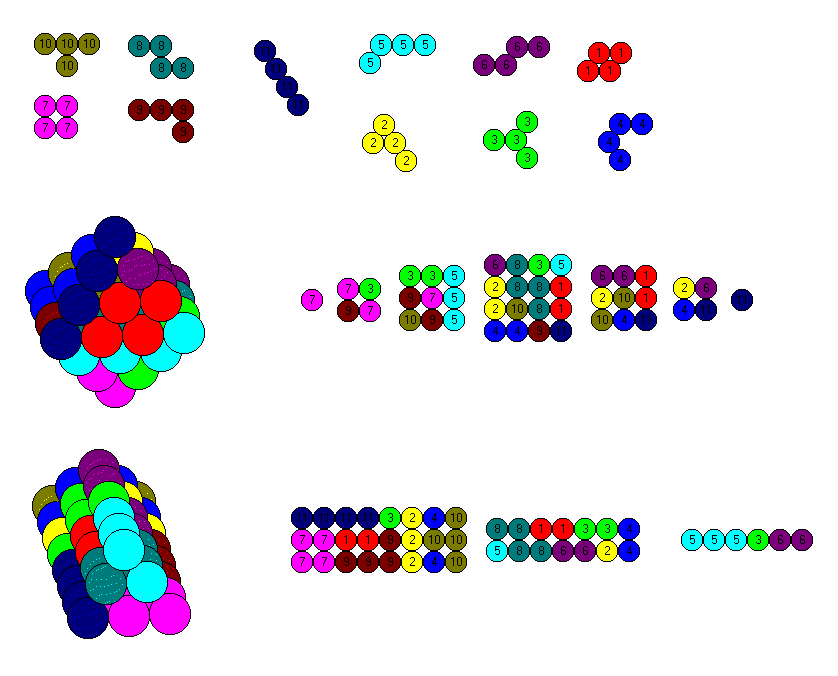
If we add the four trispheres, some more constructions are possible. A size 6 tetrahedron and a 3x10 roof are shown. You can find some more figures at Thorsten Sillke's site .
The non-planar tetraspheres make a rather difficult set. Even with a computer solution it's hard to distinguish the different pieces and put them together. I think it's a good idea to divide the set into three parts: the symmetric pieces, the pieces containing an L-tromino and the rest.

The hexagonal layers for a size 6 tetrahedron and the square layers for a 3x10 roof are shown.
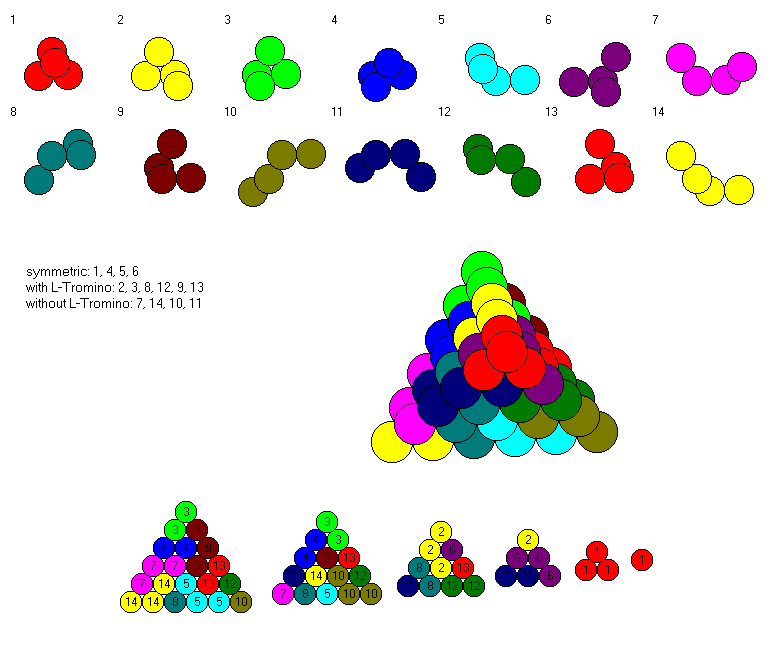
Glueing the pieces together wasn't that easy because the 2-dimensional pictures of some pieces are a little bit ambiguous. But finishing the whole construction was great fun.

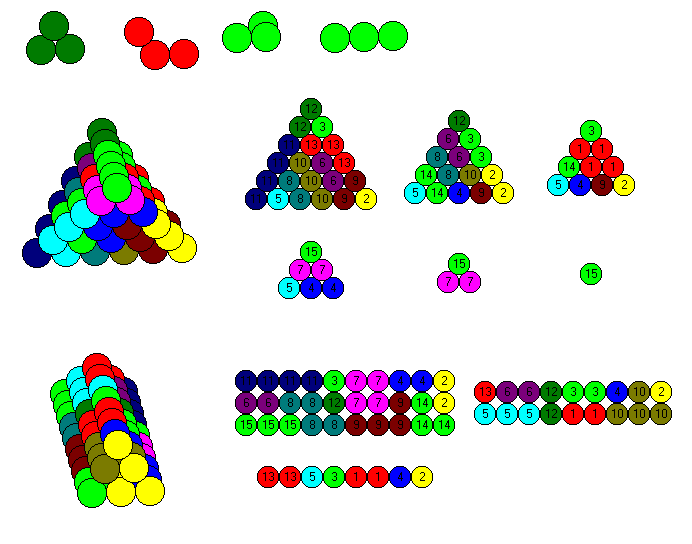
We get 25 pieces with a total of 100 spheres. We can arrange the pieces in a 8x5 roof as shown below, but I think the combination of an octahedron with planar and a tetrahedron with non-planar pieces is nicer.
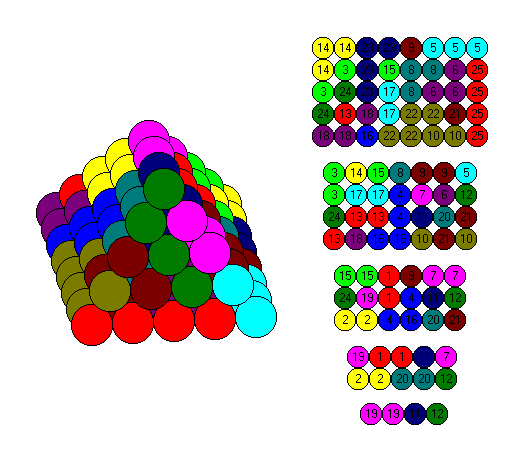

Index
Home