Pentaspheres



Here are all planar pentaspheres. The set is the union of the 22 pentahexes and the 12 pentominoes with the straight piece in both sets. So we get 33 different pieces.



Using only the 22 pieces, which are planar in the hexagonal grid we can make a 3x19 roof and a 4x12 roof or two size 6 tetrahedrons with the top sphere missing.


Two sets of the pieces planar in the hexagonal set have a total volume of 2x22x5 spheres and a size 10 tetrahedron can be made.



Using all 33 planar pieces some multiple constructions are possible. I got three square pyramids and three size 6 tetrahedrons each with a missing corner. For the pyramids I colored the table tennis balls to have three different puzzles.



Here are the layers for the multiple constructions and a single size 9 tetrahedron.



The truncated tetrahedrons are joined at the missing corner.



Adding the non-planar pieces we have 210 pieces, which allow for six 10x6 roofs but glueing all the pieces seems to be rather hard.



The layers are here.

Added 2015/3/12


In 2009 I decided to glue all 210 pentaspheres. I started with a pair of mirrored pieces, which can be combined to get a small tetrahedron of size 3. The pieces are partly wrapped around each other and must be elastic to snap into place. You must be cautious not to break the connections between the spheres. This works rather well with table tennis balls but they seem to be too large for constructions with all 210 pieces. Therefore I also tested other materials.



Marbels are small and too sturdy, spheres of wood must be connected by little sticks and drilling holes wasn't precise enough to get the right directions. At last I chose rubber balls stuck together by hot glue or silicone bonding. With the help of my computer program I constructed 21 roofs with 10 pieces each and glued the pieces according to the given layers.



The pieces were numbered by the computer program and I wrote these numbers on the pieces, because otherwise it's difficult to distiguish them. The set produced by the computer is shown so that the orthogonal grid structure is parallel to the horizontal plane and the spheres are represented as little cubes.



Here are the real pieces with the pentomino like polyspheres at the bottom of the picture.



To display the 21 roofs I built a shelf with seven rows for three roofs each.



You can also get a single roof of size 9x26. The layers are here.



If you like square pyramids and want to use all pieces you can combine different sizes. I constructed three pyramids of size 2, 4 and 10 and four pyramids, two of size 7 and two of size 10.

What about tetrahedrons? For the following ones the total of spheres is a multiple of five and constructions are possible.

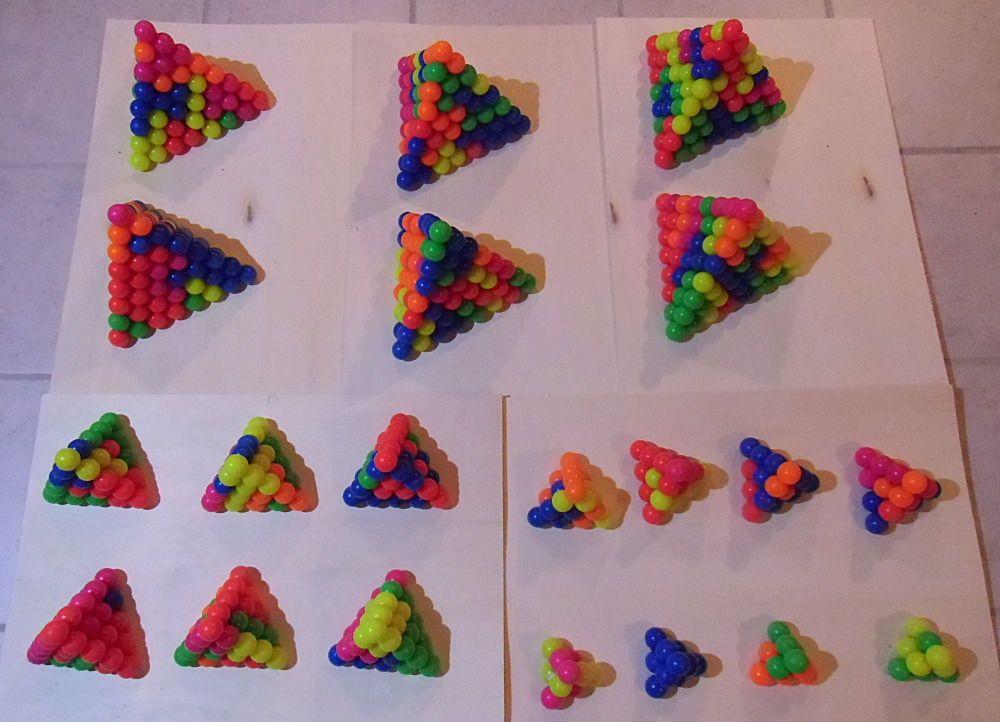
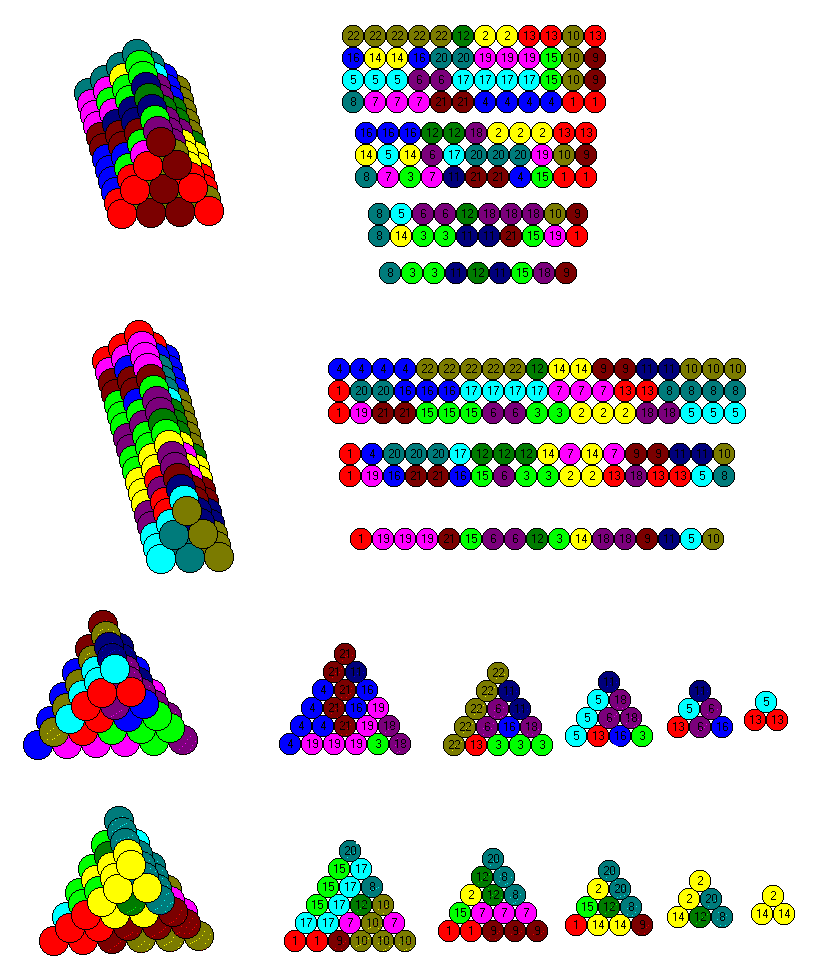
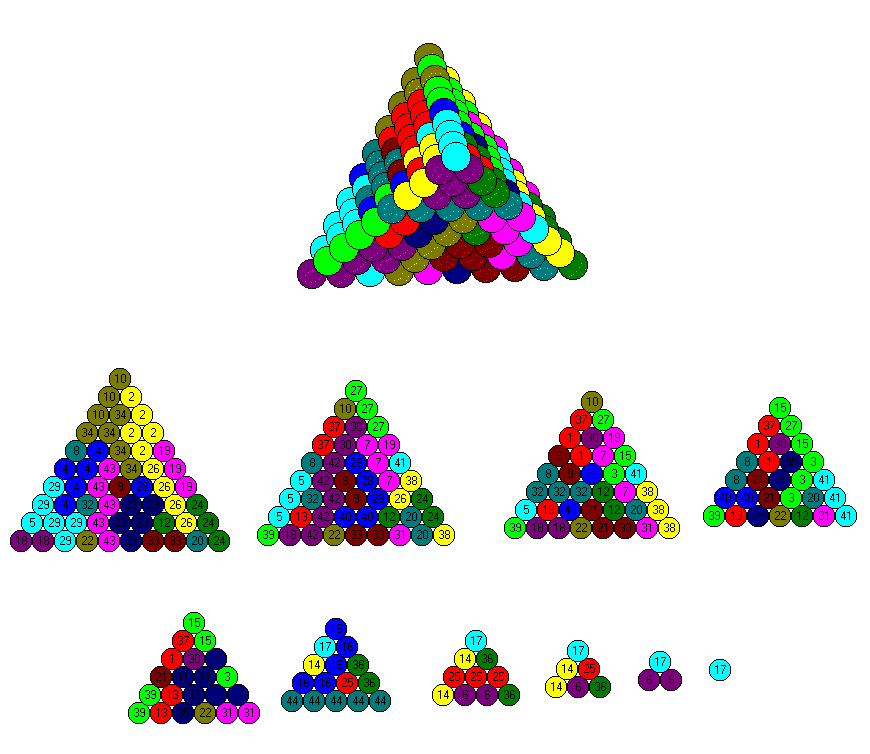
Size 3458910131415
Total Number of Spheres 102035120165220455560680
Number of Pieces 24724334491112136


I looked for combinations of tetrahedrons using all pieces and got examples for up to twenty tetrahedrons. Click the table to see the hexagonal layers.

Number of Tetrahedrons Set of TetrahedronsNumber of Pieces
3 T13 + T5 + T14112+91+7 = 210
4 2*T13 + T8 + T42*91 + 24 + 2 = 210
5 T15 + T10 + T8 + T4 + T3136 + 44 + 24 + 4 + 2 = 210
6 2*T13 + 4*T52*91 + 4*7 = 210
7 T14 + 2*T10 + T4 + 3*T3112 + 2*44 + 4 + 3*2 = 210
8 T14 + 2* T10 + 5*T3112 + 2*44 +5*2 = 210
9 2*T13 + 7*T42*91 + 7*4 = 210
10 2*T13 + 6*T4 + 2*T32*91 +6*4 2*2 = 210
11 2*T13 + 5*T4 + 4*T32*91 + 5*4 + 4*2 = 210
12 2*T13 + 4*T4 + 6*T32*91 + 4*4 + 6*2= 210
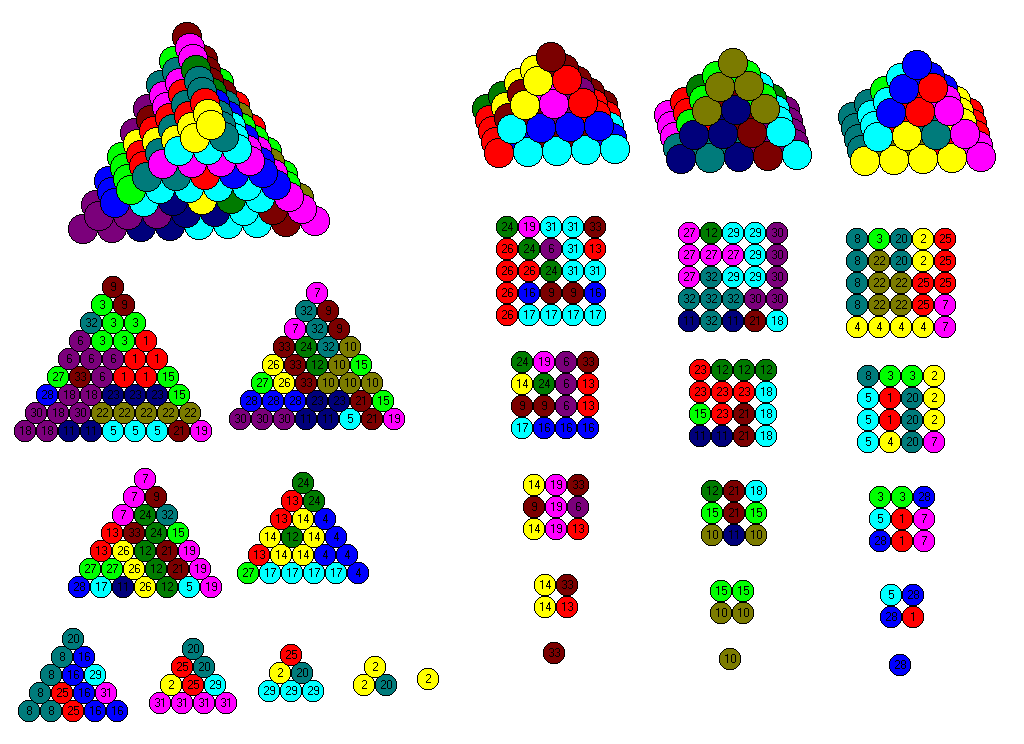
13 8*T8 + 4*T4 + T38*24 + 4*4 +2 = 210
14 8*T8 + 3*T4 + 3*T38*24 + 3*4 +3*2 = 210
15 8*T8 + 2*T4 + 5*T38*24 +2*4 +5*2 = 210
16 7*T8 + 4*T5 + 2*T4 + 3*T37*24 + 4*7 + 2*4 + 3*2 = 210
17 7*T8 + 4*T5 + T4 + 3*T37*24 + 4*7 + 4 + 5*2 = 210
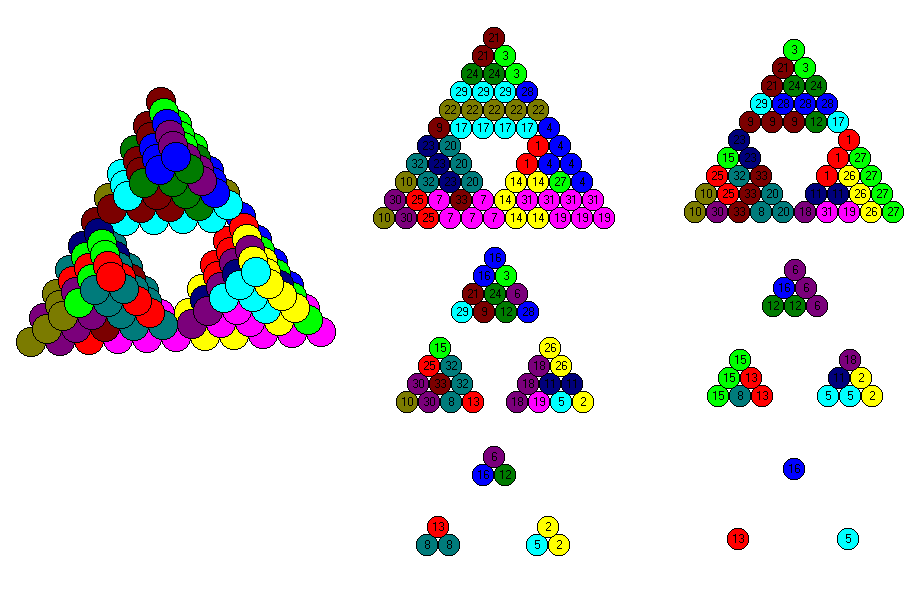
18 6T8 + 8T5 + T4 +3T36*24 + 8*7 + 4 + 3*2 = 210
19 6T8 + 8T5 + 5T36*24 + 8*7 + 5*2 = 210
20 6T8 + 6T5 + 4T4 + 4T36*24 +6*7 + 4*4 + 4*2 = 210


As late as 2015 I took the rubber pieces and built a combination of 6 tetrahedrons using the computer solution found years ago.



In the picture below you can see, how the computer solution was found. The large tetrahedrons were split into three parts separated by planes with orthogonal grid to ease the solution.



To construct the set of 20 tetrahedrons the small ones were solved first saving a lot of easy to use pieces for the six tetrahedrons of size 8. These tetrahedrons were split into two halves, because it was easier to solve twelve halves than six whole tetrahedrons.



Index
Home