

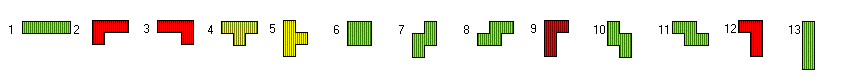
Unfortunately we have four L-tetrominoes and one T-tetromino, which get an odd number of black and white squares, if placed on horizontal striped areas. A 13x4 rectangle has 26 black and 26 white squares if horizontal striped and therefore it can not be filled with an odd number of black and white squares given by the pieces. The same argument applies to a complete ring with 13 sectores and a height of 4.
If we add a copy of one L-tetromino to the set we get 56 squares with an even number of black and white squares. So we can construct 14x4 rectangles and 7x8 rectangles or corresponding rings. Adding a copy of one T-tetromino doesn't work, because under usual checkerbooard coloring the extended set has an odd number of black and white squares.
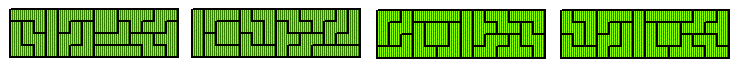
Adding the four one-sided, polarized trominoes we have 52+4*3=64 squares, and we can make 8x8 or 16x4 rectangles. Adding trisectors allows for complete rings of corresponding size. In this case the center angle of the sectors is 360°/8 or 360°/16, respectively.

I prefered constructions with 5 notched wheels to get a double ring. 3 wheels contribute 2 notches each and 2 wheels contribute 1 notch each. This way we have 52+3*2+2*1=60 =12*5 sectors in the outer ring. At first the notched wheels were placed and fixed by a gear wheel, and then the 13 tetrasectors must complete the construction.

What are allowed positions for the notches? A necessary condition for the single notches is: a) the difference between the column positions must be even and b) the difference between the row positions must be odd. Some examples are shown. Is the necessary condition even sufficient?

Solutions can also be shown by the layers of the cylinder.


With these pieces you can construct seven towers of height 5, which can be combined to get a tower of height 35.

Since the single pieces are difficult to spot in the 3d-picture all layers of the construction are also shown.
Using the corresponding set of 35 one-sided polarized pentominoes we can cover five rectangles of size 7x5 or 5x7, which can be combined to get 35x5, 25x7, 5x35 and 7x35 rectangles. To transform these solutions into complete ring figures center angles of the sectors must be 360° divided by 35, 25, 5 or 7, respectively.

From the seven 5x5 towers you can't get a solution for seven 5x5 squares, because there is no common separating radius for three (1, 2, 7) of the seven towers.
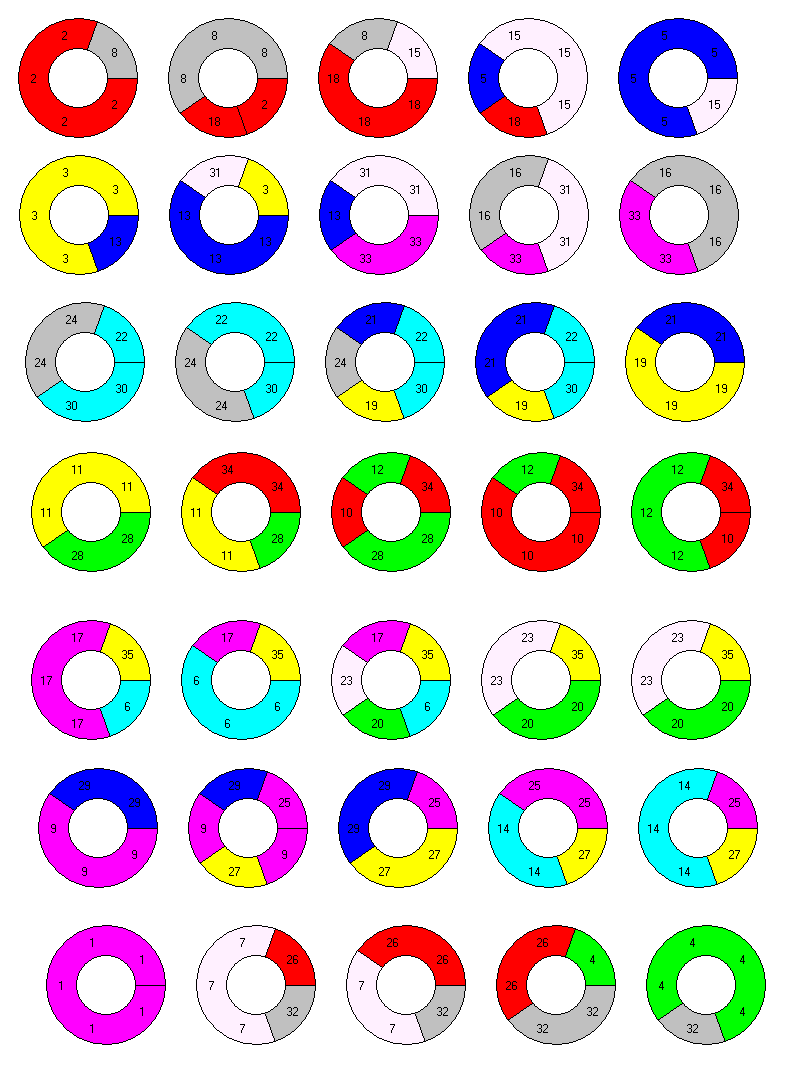
Let's add an additonal copy of one piece. The total of 36*5=180 sectors factorizes very well and many constructions of rings or sectors of rings are possible. I took the one-sided polarized pieces, added another X-pentomino and got multiples rectangles of different sizes ( 9x5, 12x5, 10x6 ). Pentasectors with center angles of 360° divided by 5, 6, 9, 10, 12, 15, 18, 30 or 36 can now be used to create rings. To change a NxM construction into a MxN one is no problem, because for each vertical striped piece there is a horizontal striped twin piece and the X-pentomino is it's own twin.

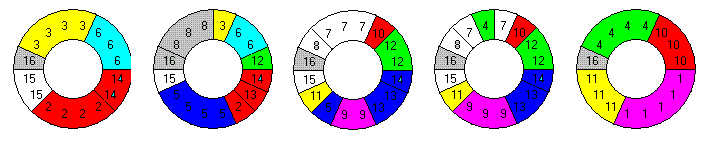
Instead of one additional pentasector we can also add a single 10°-sector in each layer of a 36x5 ring. Even if the positions of the single sectors are fixed, perhaps by notched wheels with one notch, it seems to be possible to finish the construction in most cases. If the single squares in the corresponding rectangle split the area into two parts and each part hasn't an area which is a multiple of 5, the construction failed, because the vertical I-pentomino can't be placed in either parts. Three examples are shown.

For handsolving the set seems to be a little bit too large. So you may choose 10 pieces of the set and 5 notched wheels with two notches at distances of 1, 2, 3 ,4 and 5. In total there are 10*5+5*2=60 sectors in the outer ring and 5 solid circles in the inner ring, and we can make a 12x5 ring of pentasectors with a center angle of 30°. The printed version of this is already shown on the title page, the layers are here.

Since some of the chosen pieces have an overhang I had to print them with support or I had to print parts of them, which were glued together. So I looked for the 16 pieces without overhang. Among them there are pieces like the Y-pentasector which are only included in one or two orientations. Therefore a solution for a NxM ring can't be derived from a MxN solution. With a total of 80 sectors possible constructions are rings of size 5x16, 8x10,10x8 and 16x5. If complete rings are wanted the center angels of the sectors must be 360° divided by 5, 8, 10, 15, respectively. Here are the layers of the rings.



There are 120 hexasectors with a total of 720 sectors. For a physical puzzle you can choose different center angles getting different sets. If the center angle is rather small a given constructions isn't a complete ring and if the center angle is too large some construction are impossible at all. Therefore all solutions are shown as rectangles with the one-sided polarized hexominoes.

Since each piece has a twin piece with a polarization orthogonal to its own, we can dervie a solution for a NxM rectangle from a MxN rectangle. Here are some multiple rectangles of size 12x12, 30x8, 36x10 and 40x9, which can be combined to get rectangles of size 90x8, 80x9, 72x10, 60x12, 40x18, 36x30 and 30x24.

The missing 120x6 and the 48x15 rectangle are also given.

Even a set of twelve 10x6 rectangles is possible. This can be used to construct twelve complete rings of hexasectors with center angles of 36° or 60° and heights of 6 or 10, respectively. Each ring should be a puzzle of its own.
