

With center angles of 60° we can construct a cylinder of height 3, already shown on the title page. The layers of a possible solution are here.

If we choose center angles of 120° we can get a tower of height 6. First we have to cut the above construction at a radius common to all layers. Then we bent out the two rings and get a box of size 2x6x3. At last the 2x6 faces of the box must be bend together to get the new cylinder with 3 segments and height 6. Here is an example for the layers.

Adding polysectors of order 1 and 2 we have 19 pieces. The 5 disectors are labeled with numbers from 13 to 17, and the monosectors get the numbers 18 and 19. Possible rings with following sizes of circumference X height are 8x3, 6x4 and vice versa.


Here are the 54 printed pieces with center angles of 30°. On the title page a complete double ring of height 2 is shown. This is a construction with only 2*2*12/4=12 pieces, and it's easy to solve by hand. Using all pieces we can make simultaneously three rings of height 2, 3 and 4. Stacked upon one anotherwe we have a tower of height 9.

Here are the layers.

Let's call this a NxM construction with N=12 segments per layer and a height of M=9. If we don't change the center angle, we can also get a 9x12 partial tower with a quarter missing from a complete tower.

With a center angle of 360°/9=40° for the pieces the solution remains the same, but the tower is complete.
Constructions of size 6x18 or 4x27 are also possible either with center angles of 60° or 90° or with incomplete towers.


For the 27x4 ring the center angle must be reduced to 360°/27 or less.

Instead of towers I also looked for some stairs or towers with battlements. Unfortunately the printed pieces weren't precise enough to prevent these constructions from crashing.

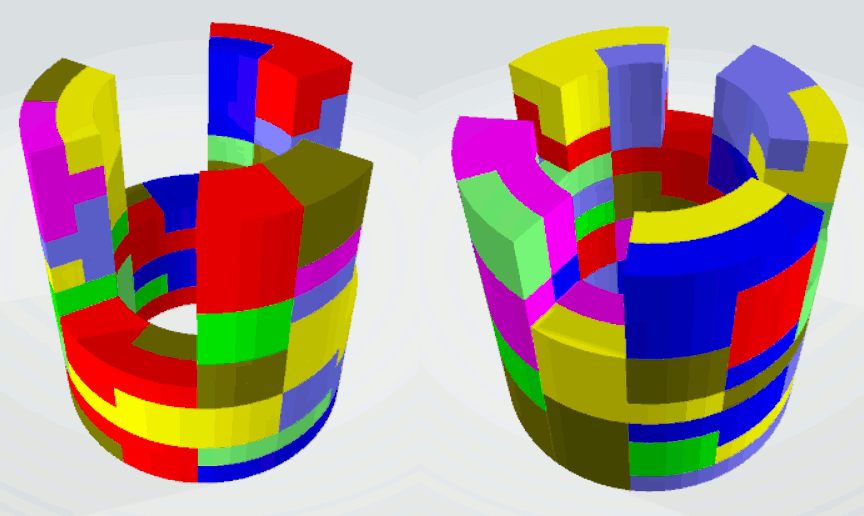
Adding pieces of lower order to the tetrasectors facilitates solving. The set of trisectors and tetrasectors has a total of 252 sectors and allows double rings of size 6x21, 7x18 and 9x14. From these solutions you can derive solutions for rings with circumference and height exchanged.

There are 73 polysectors of order 1 through 4 with a total of 264 sectors. Double rings of size 6x22 and 11x12 and vice versa are possible to make. In the pictures of the layers the numbers of the pieces depending on their order are 1:72,73; 2:67..71; 3:1..12 and 4:13..66.


l

This construction can be transformed into a ring with 360°/107 sectors. For example the two pieces which are complete rings change into vertical I-pieces and the vertical I-pieces change into horizontal almost straight I-pieces.