Planar Tetrarhons
There are 14 planar tetrarhons. Nine pieces can only be used for planar polyhex figures, four pieces (2, 7, 8, 9) only for
planar polyomino figures and the straight piece for both.

Like the tetrominoes the five planar tetrarhons suitable for polyomino figures can't be used to
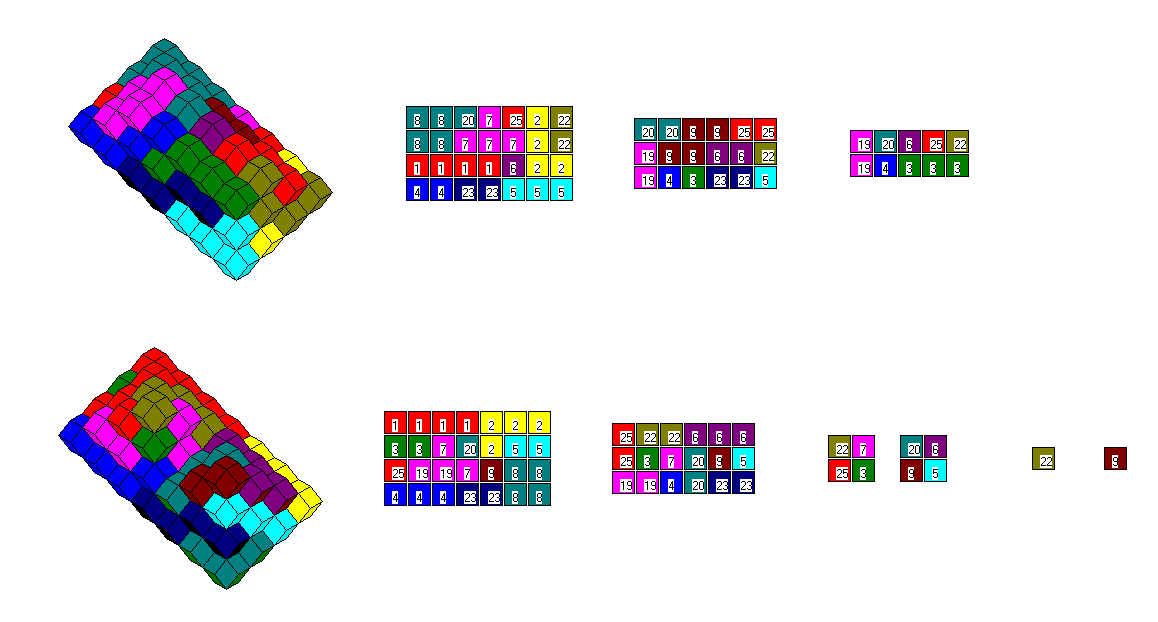
construct a rectangle because of a checkering argument. Let's have a look at the ten planar tetrarhons suitable
for polyhex figures. They are different from the one-sided tetrahexes because there are two star tetrarhons (20, 25)
but only one star tetrahex. Furthermore there is only one S-tetrarhon (23) but two one-sided S-tetrahexes.
Without the straight piece, we have a total volume of 9*4=36 rhombic dodecahedrons, just enough to
make a triangle, a rhomb, a parallelogram and an hexagon with a center hole.

Adding the straight piece we have 40 rhombic dodecahedrons and can construct two parallelograms, a trapezium
and a small long hexagon.

As a 3-dimensional object you can see a 4x5 roof.

The whole set of planar tetrarhons can be used to make a tetrahedron of size 6 as shown in the title.
Even with the given layers it isn't that easy to finish the construction.

For the following figures click the pictures to get the layers.
The shown kind of pyramid has an additional rhombic dodecahedron on the top. This is
only possible if rhombs touch the bottom and therefore the two units of the top are
also connected by rhombs.

Square pyramids of size four have a volume of 30 units. If we omit one unit at two
bottom corners we can get two congruent pyramids with the set.

Removing all bottom corners of a 3x6 roof we have a volume of 28 units and can
make two congruent constructions.

Starting with a 6x7 bottom layer a flat top or two peaks at the top are possible.
Beside the 3x10 roof we can get three L-shaped roofs.

You can ty to make kind of boxes. If you start with an a x b layer, the next layer may be
(a-1)x(b-1), (a+1)(b-1), or (a-1)(b-1). Now you alternate the layer sizes ending with
a top layer congruent to the bottom layer. This gives a symmetric figure looking
like a block or box.
If rhombs instead of corners are on the bottom there is a better chance to get a stable
physical construction. Three examples are shown.

Back
Home











