Nonplanar Tetrarhons

Here are the 14 nonplanar tetrarhons.

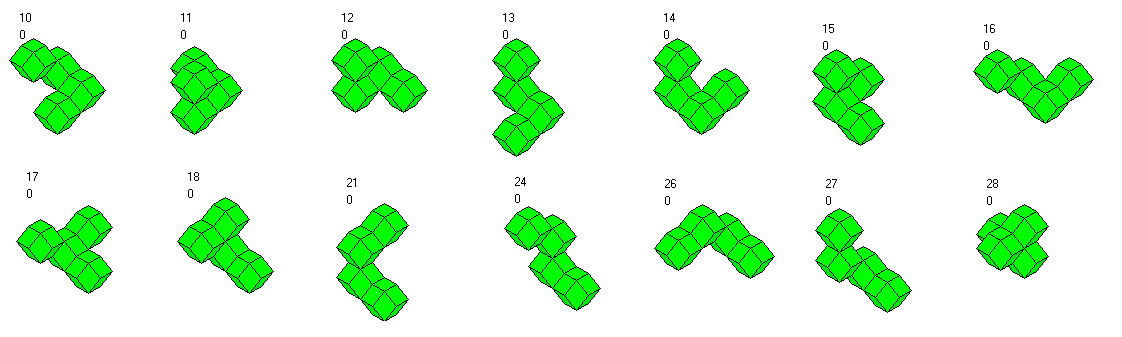
It's difficult to distinguish the pieces, but you can divide the whole set in subsets with four symmetric pieces and five mirror pairs. Then you can check wether a V-trirhon, a triangle trirhon or only arc trirhons are part of the pieces.

11,17, 18, 28: symmetric
12,15: triangle trirhons are part of the pieces
24, 27 only arc trirhons are part of the pieces and they are S-shaped
21, 26 only arc trirhons are part of the pieces and they are C-shaped
13, 16 the V-trirhon is part of the pieces and they are S-shaped
10, 14 the V-trirhon is part of the pieces and they are C-shaped

Sometimes you get a solution, where all places of a figure are covered by the pieces but the physical construction failed. The first picture shows the pieces 10 and 27, which can be put together if one piece is moved in one special direction. This direction may be blocked by a third piece so that you have to change the order of assembling or can't finish the construction at all. Even worse is the situation in the second picture. The pieces 10 and 26 don't fit together although they would cover different positions.

For the construction of a tetrahedron shown in the title fortunately such problems didn't occur. Below are the layers for this tetrahedron of size 6.

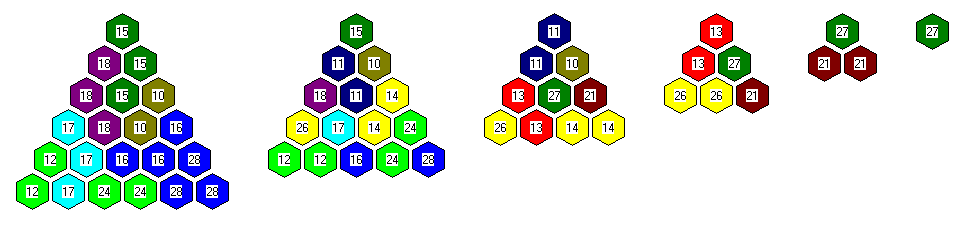
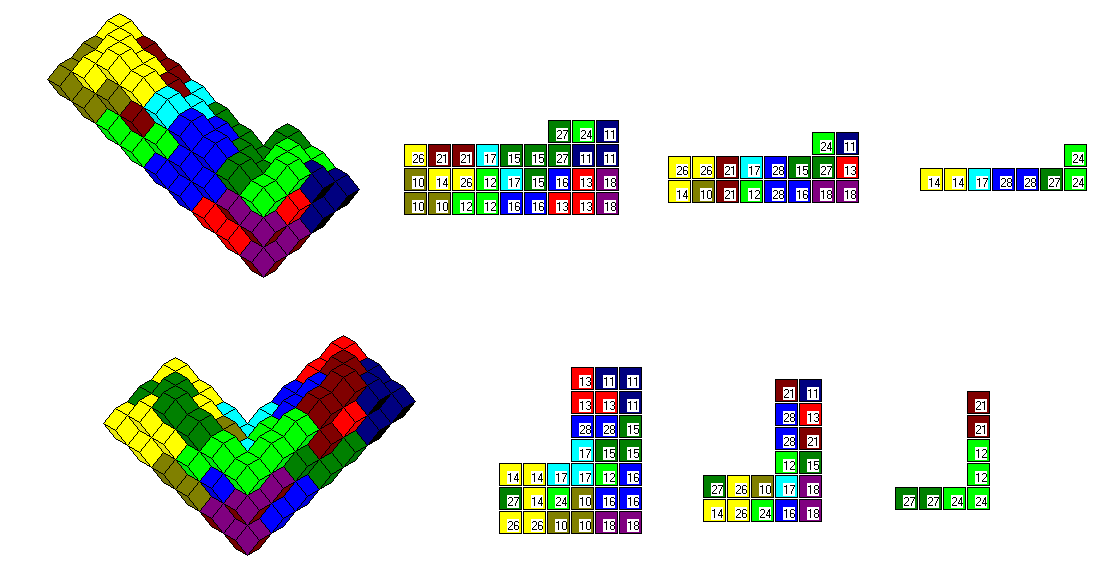
Many other constructions made with the planar tetrarhons are also possible with the nonplanar tetrarhons. Click the pictures to see the layers of the solutions.

Among the I- and L-shaped roofs made with the planar pieces only two L-shaped roofs are possible to construct with the nonplanar pieces.

Back
Home