Above there is the printed version of the pieces arranged as a 7x7 square. I chose a unit length of 2cm with a small inset and a thickness of 1.2 mm, and you can download the obj-files here.
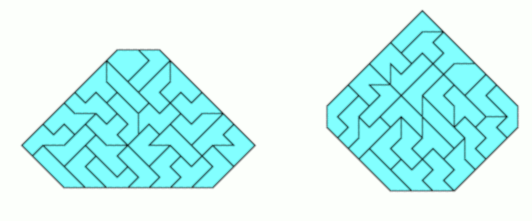
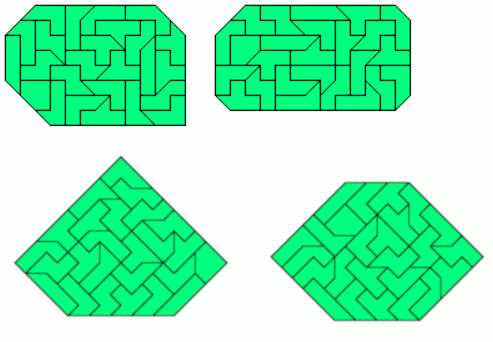
Among convex polygons there are symmetric hexagons and octagons.
A convex pentagon and heptagon are also possible but not symmetric.

Symmetric but not convex are the following jagged figures.
For all 14 pieces you can construct a 9x7 rectangle with a hole shaped like a 2-fold copy of the pieces. All solutions are here.


Even a symmetric hexagon and a symmetric heptagon are possible.
Discarding any of the 27 pieces the remaining 26 are able to make a 13x7 rectangle. All solution are here.

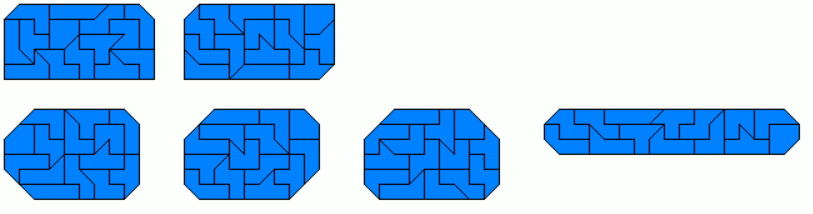
Rectangle of size 14x7 with a hole shaped like any of the pieces can also be made. All solution are here.

For all but one piece you can create a 14x9 rectangle with a hole shaped like a 3-fold copy of the piece. All solution are here.


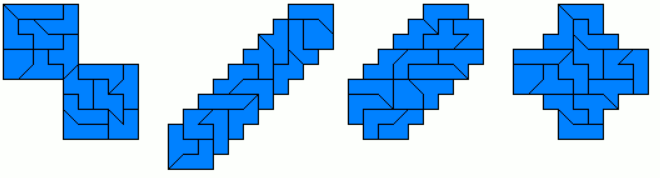
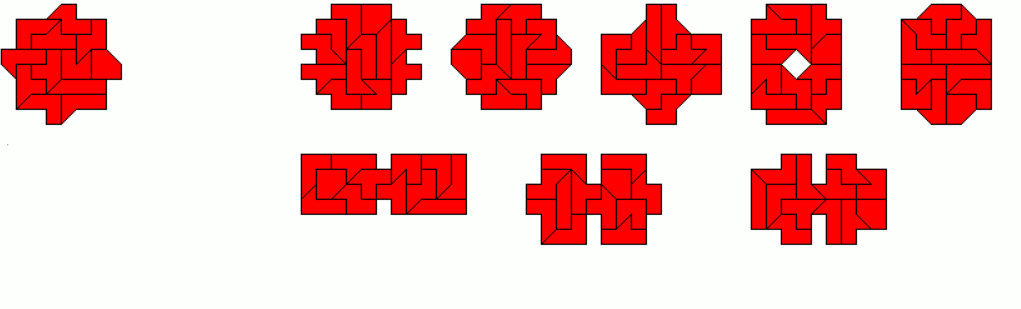
Here are some examples with rotational or mirror symmetry.
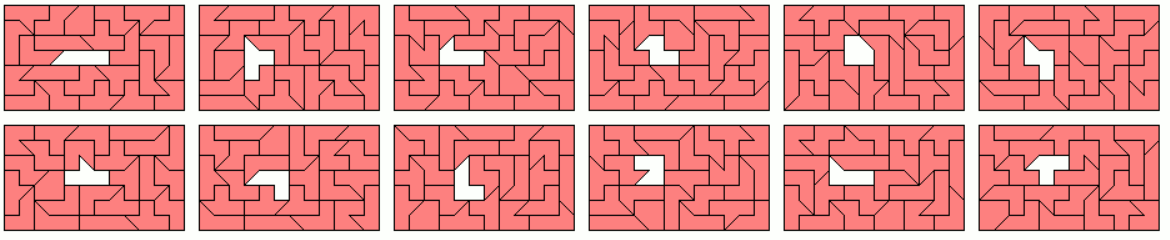
I tried to construct 7x8 rectangles with a hole shaped like a 2-fold copy of any piece. But this didn't work for three pieces at least if the hole must be completely surrounded by pieces.

At last I constructed 7x12 rectangles with a hole shaped like the pieces. This can be done for all pieces.
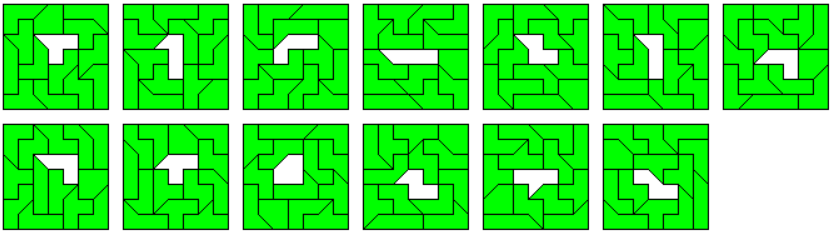
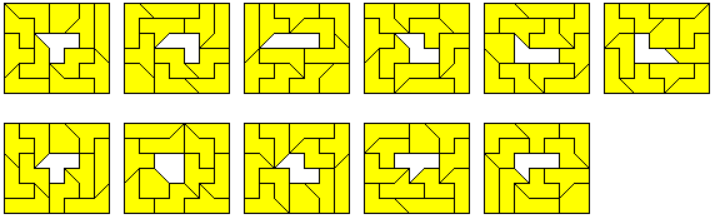
For this set you can construct 7x7 squares with holes shaped like the pieces.
If the total area isn't integer, you can add a second copy of one piece or let a hole as large as a piece and then you have an integer area. This area is often the area of a rectangle and hole constructions can be made. For this set rectangles of size 13x7 are suitable.
Because we have 25 pieces 5-fold replicas of them might be possible. But that is only true for pieces without a sharp angle.

Now 7x6 rectangles with holes shaped like the pieces can be made.
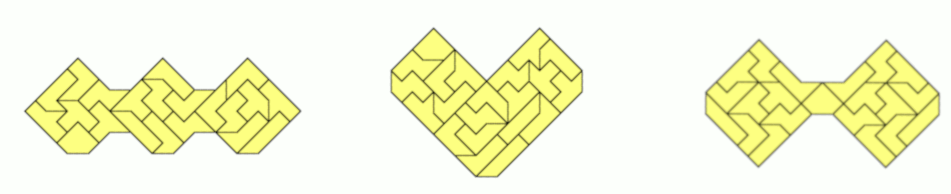
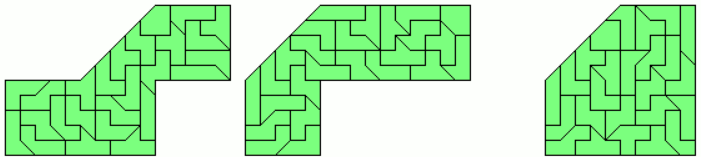
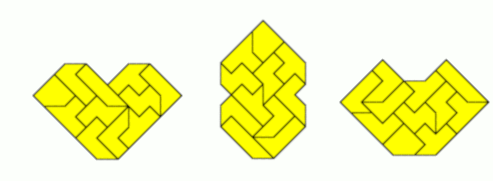
At least three figures with one axis of symmetry are shown.
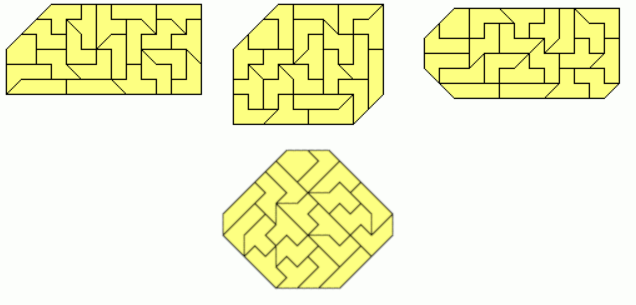
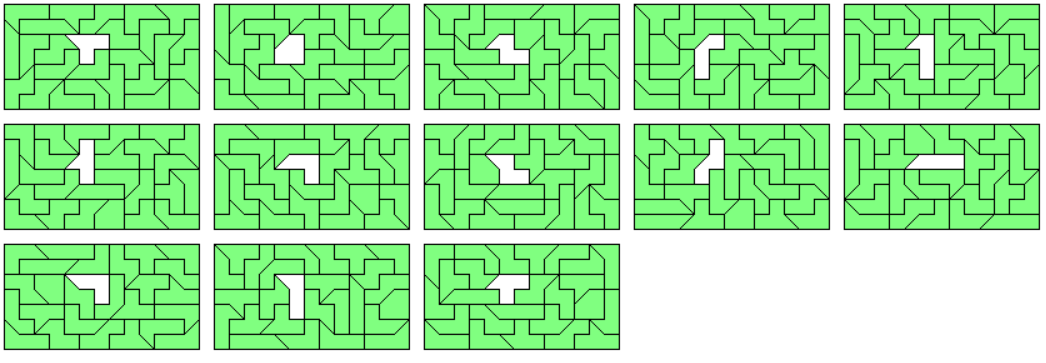
In a rather large rectangle of size 11x7 it's no problem to get holes shaped like the pieces.
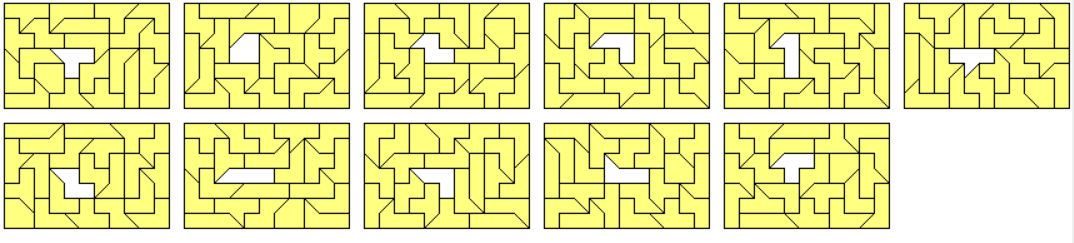
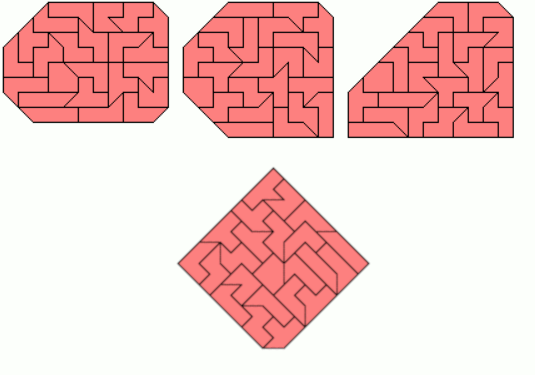
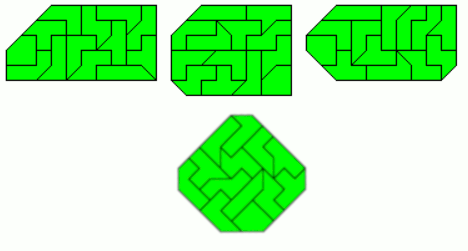
I also constructed three examples of figures with one axis of symmetry .