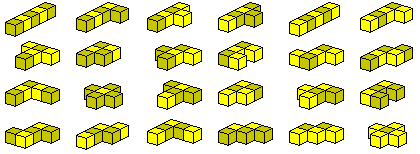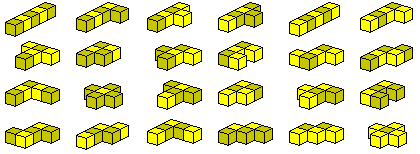Chequered Solid Pentominoes
Let's chequer the solid pentominoes. Since each piece consists
of an odd number of cubes we have two possibilities to chequer it and
we get 24 different pieces and a total volume of
120 unit cubes .
Here are the pieces.
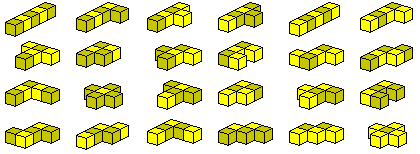
A lot of constructions can be done if you start with a figure
made from the solid pentominoes then make another copy or a reflected
copy with changed colors and put the original and the copy together. Many
boxes e.g. 2x3x20, 2x5x12, 2x6x10, 3x4x10, 3x5x8 and 4x5x6 can be found this way.
All towers of height 6 with a double-sized pentomino as cross-section are possible,
too. For the X and W-pento the construction can't be derived from a height 3 model because these
models are impossible with solid pentominoes. But the enlarged constructions with chequered pieces can
be done and are shown in the applet below.
The same applies to the Taylor cross (a cross with a 2x2 hole) and
a 9x9 rectangle with a 7x3 hole . Both patterns can't be made with pentominoes but a construction with two
layers and the chequered set are possible and shown.
Some square rings are also shown. I chose only those rings, where the numbers of cubes at all edges are odd.
In this case you can't simply make a construction for half the figure to
join two copies for the whole ring.
At last there are some 3-fold replicas of the solid pentominoes. Since 27*5-120=15 a similar hole is left in the cross-section.
5x5x5 cubes with a mould for a pentomino at one face seem to be possible too.
Click the pieces to remove them from the construction and click the single piece to put it back.
If you combine cubes of different wood you can rather easily make the pieces.