| Number of Notches | Number of Pieces | Total Area | Constructions | |
|---|---|---|---|---|
| Two-sided Pieces | k odd | 1/2*(10Ck + 2*(4C((k-1)/2))) | 2*(10Ck + 2*(4C((k-1)/2))) | |
| k even, k>0 | 1/2*(10Ck + (4C(k/2)+(4C((k-2)/2))) | 2*(10Ck + (4C(k/2)+(4C((k-2)/2))) | ||
| 0 | 1 | 4 | ||
| 1 | 6 | 24 | no rectangles, 6 isn't a multiple of 4 | |
| 2 | 25 | 100 | no rectangles, 25 isn't a multiple of 4 | |
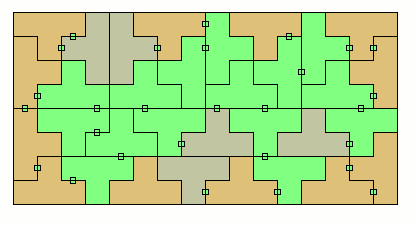
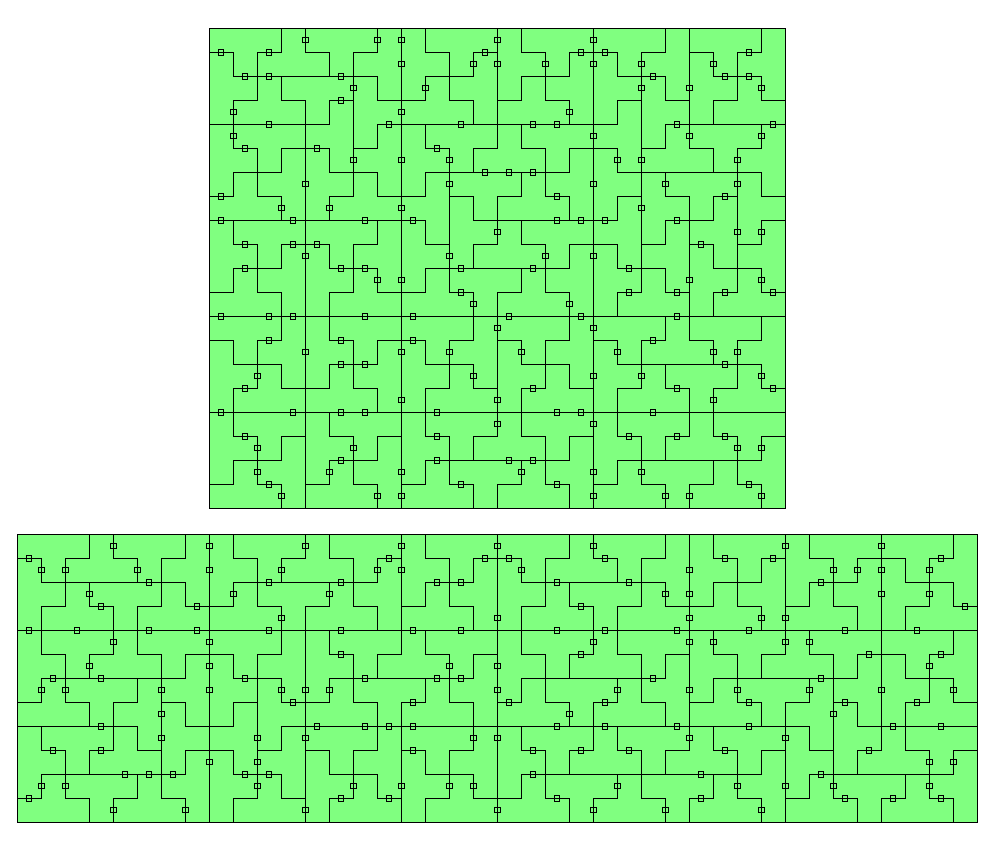
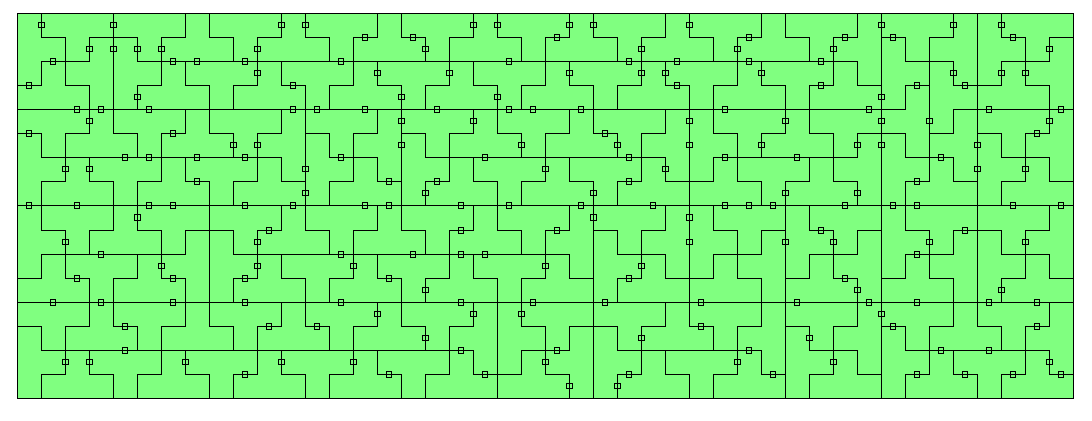
| 0..2 | 32 | 128 | 8x16 rectangle | |
| 3 | 64 | 256 | 16x16 square | |
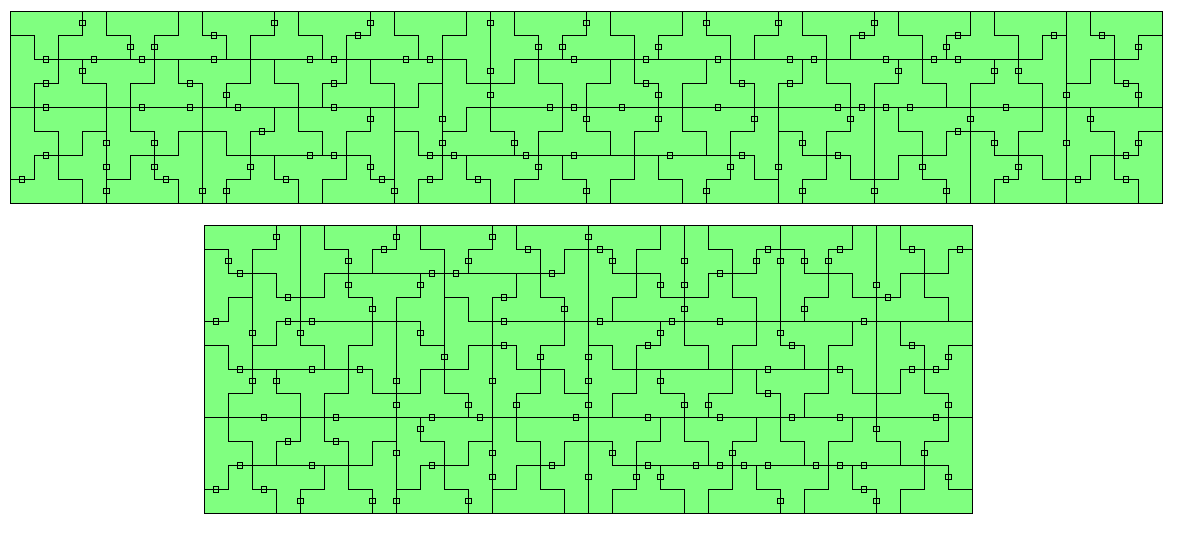
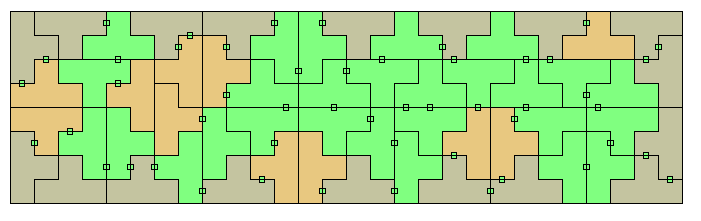
| 0..3 | 96 | 384 | 8x48, 12x32, 16x24 rectangle 20²-4² square ring |
|
| One-sided Pieces | k | 10Ck | 4*(10Ck) | |
| 0 | 1 | 4 | ||
| 1 | 10 | 40 | no rectangles, 10 isn't a multiple of 4 | |
| 2 | 45 | 180 | no rectangles, 45 isn't a multiple of 4 | |
| 0..2 | 56 | 224 | 8x28 rectangle | |
| 3 | 120 | 480 | 12x40, 20x24 rectangle | |
| 0..3 | 176 | 704 | 8x88, 16x44 rectangle |