Notched Square-tetrominoes





The picture above shows a symmetric figure made from all notched square tetrominoes. You can't get a rectangle with these pieces, because the number of straight square sides is odd. Shifting rows of squares by half the length of the square side allows to match one straight square side with notch free halfs of two other squares.

Is there a set to cover rectangle? Let's have a look at the total number of notches and straight sides for different sets.

Number of Notches at Each Piece 0 1 2 3 4 5 6 7 8
Two-sided Pieces Number of Pieces 1 1 6 7 13 7 6 1 1
Total Number of Notches 0 1 12 21 52 35 36 7 8
Total Number of Straight sides 4 3 13 10 9 3 1 0 0
One-sided Pieces Number of Pieces 1 2 8 14 20 14 8 2 1
Total Number of Notches 0 2 16 42 80 70 48 14 8
Total Number of Straight sides 4 6 17 18 16 6 1 0 0


Beside the trivial sets only the set of one-sided pieces with three notches allows for a rectangle. The other sets have an odd number of notches, an odd number of straigth square sides or too less straight sides.

Using sets of pieces with different numbers of notches some construction of rectangles are possible and mentioned in the following table.

Number of Notches Number of Pieces Total Area Constructions
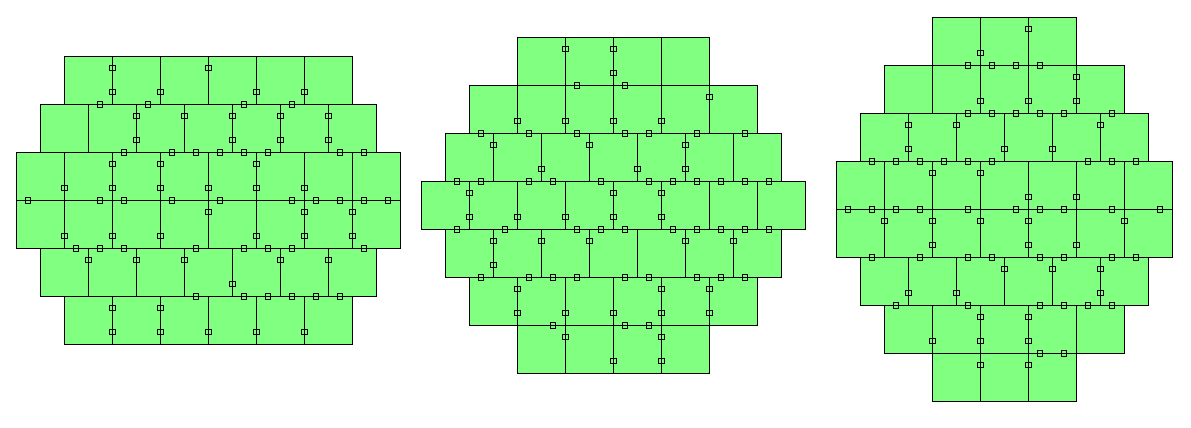
Two-sided Pieces 0..3 15 60 6x10 rectangle
0..4 28 112 some symmetric figures
0..7 42 168 some symmetric figures
0..8 43 172 stacked rows
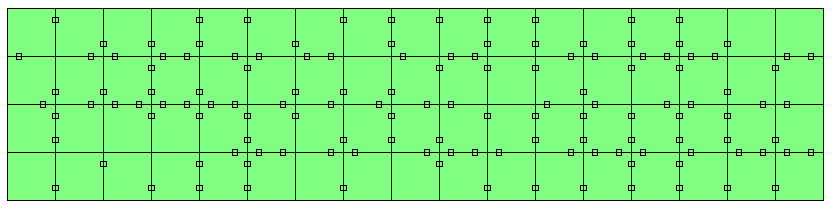
One-sided Pieces 3 14 56 4x14 rectangle
0..8 70 280 14x20 and 10x28 rectangles, stacked rows
1..7 68 272 8x34 rectangle
2..6 64 256 16x16 square, 8x32 rectangle,
8-fold replicas of tetrominoes
3..5 48 192 12x16 rectangle


Here is the set of notched square tetrominoes with up to three notches. It was cut from plywood and the notches are marked with a permanent marker.



Beside the 12x16 rectangle you can construct some other figures with one or two axis of symmetry.



The solutions are here.
If each square tetromino has 0 to 4 notches, we get 28 different pieces but the total number of straight square sides is 39. Therefore we can't construct any rectangle but some stacked rows of squares.


Sets with 0 to 5 or 0 to 6 notches have an unbalanced number of notches but the set of pieces with 0 to 7 notches can be used to construct some stacked rows of squares.


Adding the piece with 8 notches to the set of pieces with 0 to 7 notches we get a set of 43 pieces. Squares from cutting the V-trominoes were left over and I marked the notches with a permanent marker.


The total number of notches is even but the total number of straigth square sides is odd and therefore you can't pack a rectangle. Two constructions of stacked rows of squares are shown below another one using the real pieces is in the title.



The set of all one-sided square tetrominoes with three notches complies with all constraints. The 14 pieces have a total of 42 notches and a total of 18 straight square sides and a rectangle of size 4x14 can be made.



There are 70 one-sided square-tetrominoes with an arbitrary number of 0 to 8 notches. Rectangles of size 14x20 and 10x28 can be covered. The pieces are essentially the same as the edged colored squares with four possible colors, because each color can be coded by a two digit binary number. For construction other than rectangles there is a difference, if squares are shifted.



The enclosing hexagon of the stacked rows of squares is almost a regular one.



Omitting the pieces with no or all 8 notches we get a set of 68 pieces with 1 to 7 notches. We can only cover a 8x34 rectangle, because for the 4x68 rectangle 72 straight sides are needed and only 64 are available.



There are 64 square-tetrominoes with 2 to 6 notches. With these pieces you can fill a 16x16 square and a 32x8 rectangle. These figures are 16-fold replicas of the square- and I-tetromino and you can replicate the other tetrominoes, too.



The set of pieces with 3 to 5 notches contains 48 elements, but only 40 straight sides are given. Therefore only a 12x16 rectangle can be covered. A 6x32 or a 8x24 rectangle needs 76 or 64 straight sides, respectively.



Back

Home