


We have a total of 33 squares and can try to make a 11x3 rectangle. Using a computer program this isn't a real problem, but I tried to do it by hand and it took me about 10 minutes.

Since 33=32+1=4*8+1 several figures with rotational symmetry and one square in the center can be made

All Solutions are here.
Let's have a look at the 15 one-sided pieces with a total of 45 squares. The bridges are printed with a slope of 60 degrees to avoid problems with overhangs. Here are the obj-files of the pieces.

As basic geometric figures two rectangles, one jagged rectangle and one triangle are filled with the complete set.

Pentomino models three times as large can also be made. With the printed pieces I finished the X-pentomino rather fast. It is shown below the title. I think it's easier to arrange one-sided pieces than the two-sided ones. All solved pentomino models are here.
Furthermore you can try rectangles of size 5x8 with a pentomino hole.

45=49-4. Therefore you can look for a 7x7 square with 4 missing squares at best at symmetric positions. Some examples are shown.

A solution by hand with the physical pieces isn't very hard.

At last I constructed some figures with rotational symmetry around a center square.

Unfortunately there are 31 odd pieces which have an odd number of white and black squares under checkerboard coloring. So we can't construct any rectangle. I decided to discard the simple T-tetromino getting a total of 90*4=360 squares and no parity issues. Squares with square holes were easily found.

A lot of rectangles can also be made with the reduced set of 90 pieces. Six rectangles of size 4x15 can be combined to get rectangles of size 4x90, 8x45, 12x30 and 24x15.

Two 9x20 rectangles can make a 9x40 and a 18x20 rectangle.

Two 5x36 rectangles can make a 5x72 and a 10x36 rectangle.
The only missing rectangle of size 6x60 is given by two 6x30 rectangles.

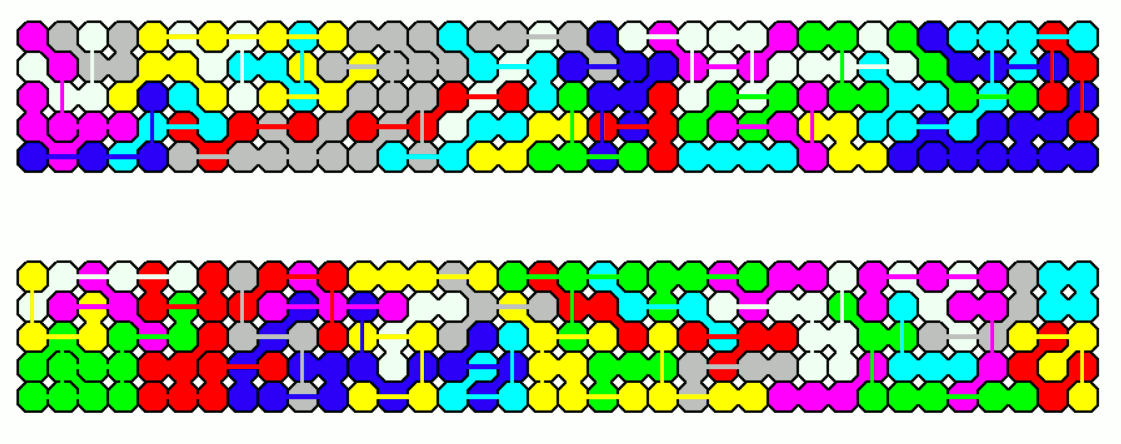
There are 156 different one-sided pieces with a total of 624 squares. Since we have 57 odd pieces rectangles aren't possible to construct. Discarding the the simple T-tetromino 155 pieces with a total of 620 squares are left. Now we can make five rectangles of size 4x31 which can be combined to get rectangles of size 4x155 and 20x31.

A rectangle of size 10x62 is also possible.

The 5x124 rectangle is split into three parts.

Also with the missing T-tetromino I constructed an almost square ring of size 25x26-5x6.

Instead of discarding the T-tetromino we can make a 30x22 rectangle and allow a hole shaped like a 3-fold model of the T-tetromino.

This should be possible for other odd pieces. Another construction starts with a 41x20 rectangle letting a hole like a 7-fold model of the T-tetromino.


We have 1614 one-sided pieces with a total area of 8070 squares. I made a snake like figure, too.

