

A 19x3 rectangle can't be made with these pieces, because one piece (a violet one) has a height of 5 rectangles and doesn't fit. A piece with width 5 (a green one) prevents the 3x19 rectangle.
But there are various constructions with two axes of symmetry.

If we add six grid elements we have a total area of 63 and can construct 7x9 rectangles with holes of six rectangles connected at their sides like hexominoes.

If the grid cells have a side ratio of 1:2 we can make a rectangle using grid change.

The set of one-sided pieces with three connected rectangles has 30 elements and a total area of 90 rectangles. The obj-files of the printed pieces are here, but solving problems by hand seems to be more difficult for this set.

Rectangles of size 5x18, 6x15 and 9x10 are possible.

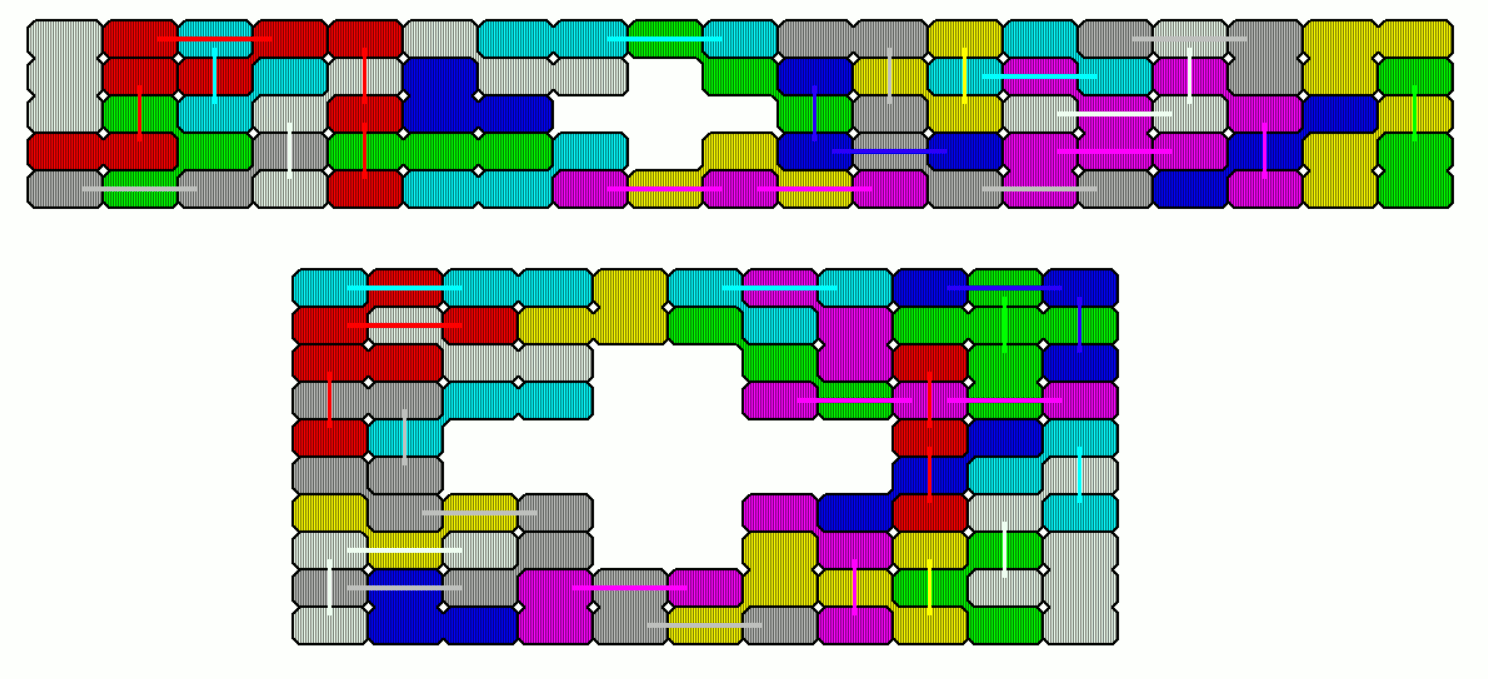
Furthermore you can get rectangles with rectangular holes.

I looked for figures with two axes of symmetry.

Pentarectangles are rectangles connected at their sides. Holes shaped like pentarectangles can be placed in some rectangles.
If the side ratio of the rectangles is 1:2, models of the pentominoes can be constructed.

With the given printed pieces only models of pentarectangles are possible.


The one-sided 319 tetrarectangles with an area of 1240 have the same parity problem as the two-sided set. Without a L-tetrarectangle I solved two 12x40 and one 12x23 rectangles to get a large rectangle of size 12x103 = 1236.
