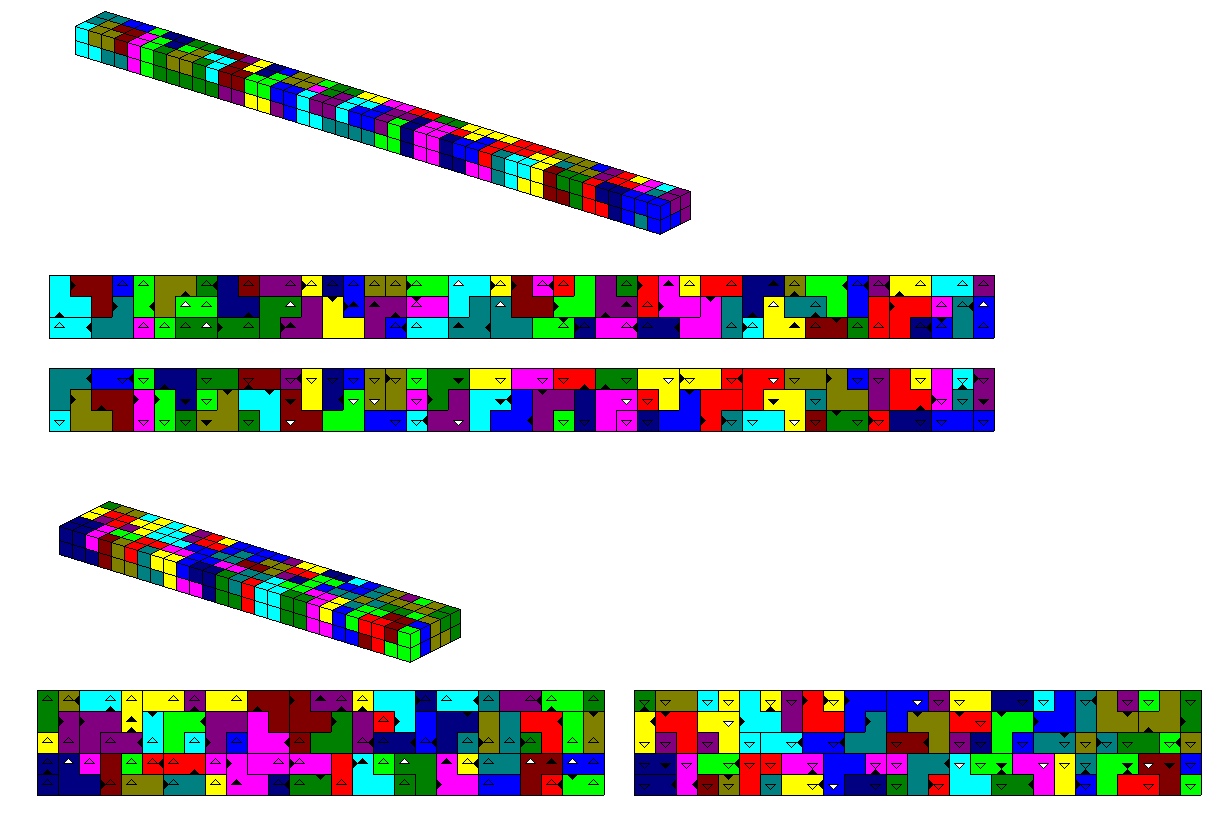V-Tricubes with Pegs and Notches
Here are the 91 V-tricubes with exactly one peg and one notch.

With this set you can't construct a box, because the number of pieces with peg and notch getting the same color
under checkerboard coloring is 41. Together with the balanced pieces the odd number of unbalanced
pieces produces different counts for non plane faces on white and black places. Therefore a match is impossible.
Jared McComb suggested to remove the piece with peg and notch at the crook (pieces number 45), because in a real
construction this pieces can hardly be used. Then we have 40 unbalanced pieces and a total volume of 270.
With this set a lot of boxes can be made. I used two 3x3x15 boxes and two 3x5x9 boxes to get
3x3x30, 3x6x15, 3x5x18, 3x9x10 and 5x6x9 boxes.
For the 2x3x45 and 2x5x27 boxes a special construction was needed.
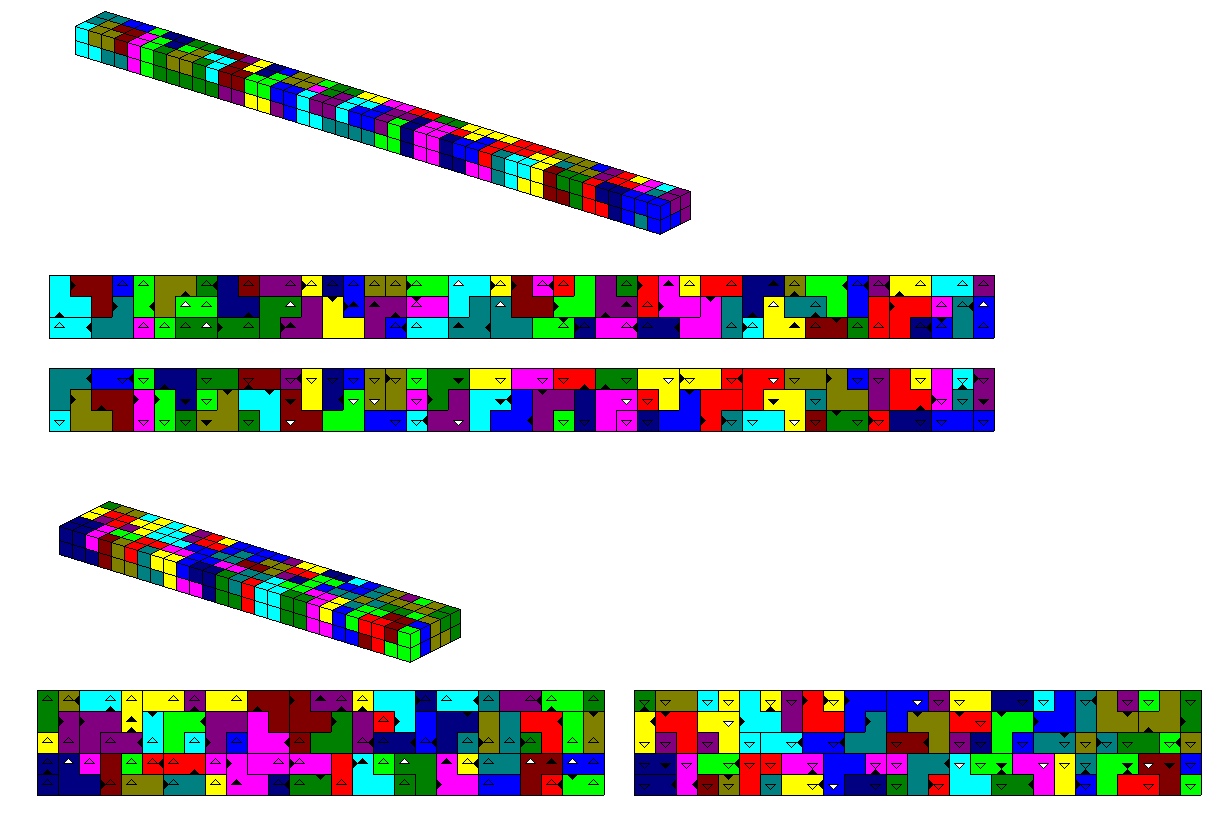
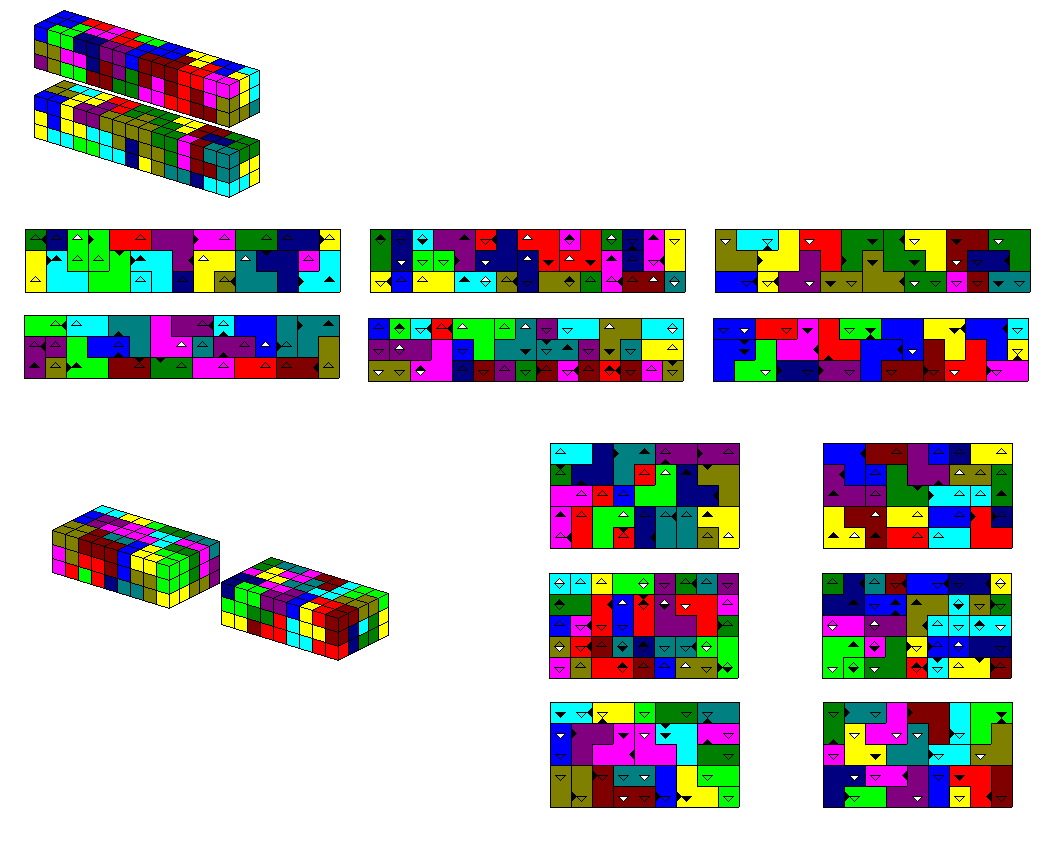
It's also possible to make models of the decominoes. I used four sets of polyominoes, so that each decomino can be
produced with at least one set.
The triplication of the pieces in the sets is shown
here.
Seven pieces with only one peg plus seven pieces with only one notch allow for a 2x3x7 box.

The computer can find a solution immediately.
If we take the 91 pieces with one peg and one notch and the 14 pieces with only one peg or notch we have
a total volume of 315 = 3x3x5x7 and can make boxes of size 3x3x35, 3x5x21, 3x7x15 and 5x7x9.

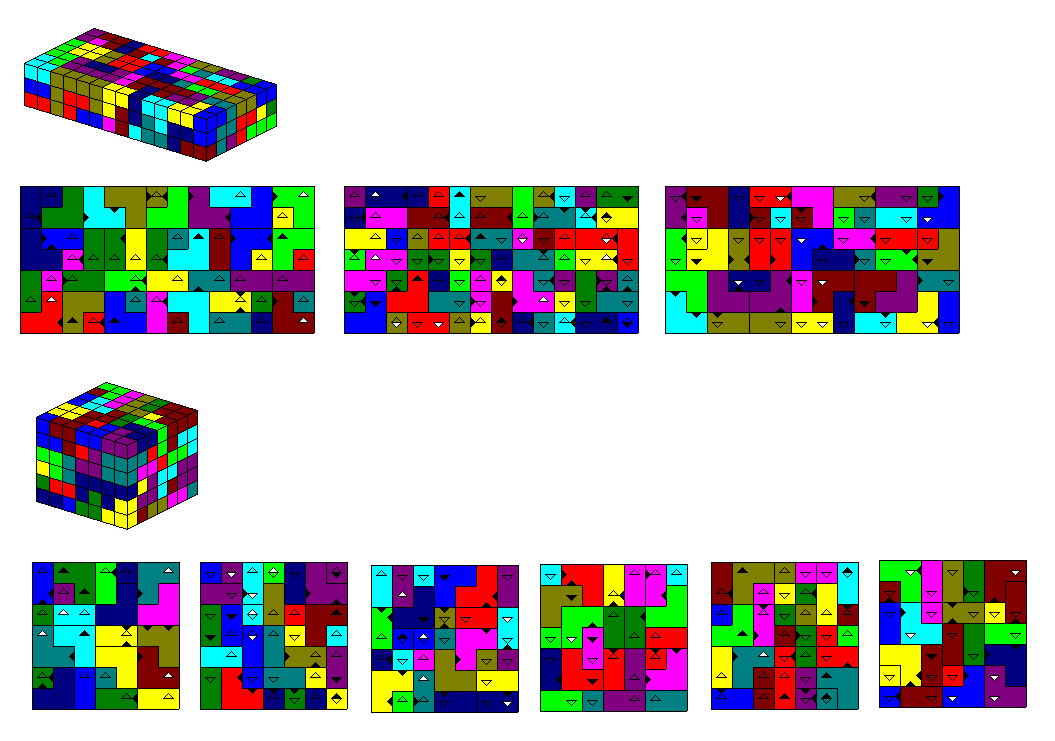
There are 49 pieces with two pegs and 49 pieces with two notches.
With these pieces you can construct a 3x7x14 and a 7x7x6 box. For the last one I split the box into
three 3x4x7 boxes and one 2x3x7 box. It's much easier to let the computer search for some smaller boxes than
for one large box.
Back
Home