Dicubes with Pegs and Notches
Here are the 12 dicubes with exactly one male face (blue colored) and one female face (red colored).

Unfortunately you can't construct a box with theses pieces. If a box gets a checkerboard coloring the number
of male and female faces at black cubes must be the same as the number of male and female faces at white cubes.
But there is an odd number of unbalanced pieces (3, 9, 10, 11, 12), so that this condition can't be satisfied.
Adding the two pieces with only one female face and the two pieces with only one male face we get 16 pieces
and can construct models of all tetracubes. Beside the one shown in the title there is only another non flat tetracube.
It is shown here with its layers.

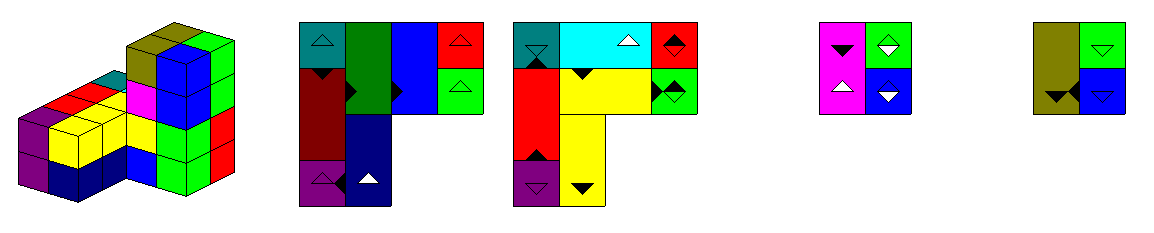
The layers of all other flat tetracubes, which can be replicated, are
here.
Among them are the possible boxes 2x2x8 and 2x4x4.
One is shown with the physical pieces.

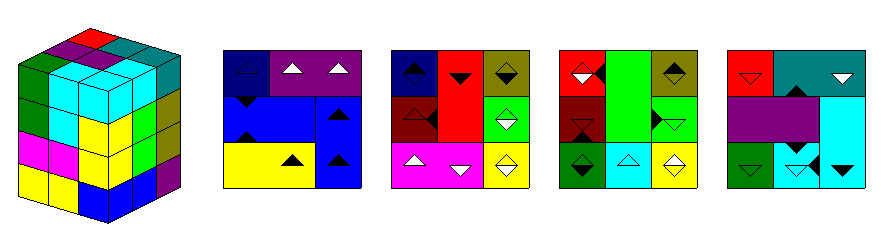
There are 9 pieces with exactly two male faces at the surface of a dicube. To match these pieces we need
another set of 9 pieces with two female faces. How fast can you assign the male pieces to the corresponding
female ones?

A 3x3x4 and a 2x3x6 box can be made with this set.

Back
Home







