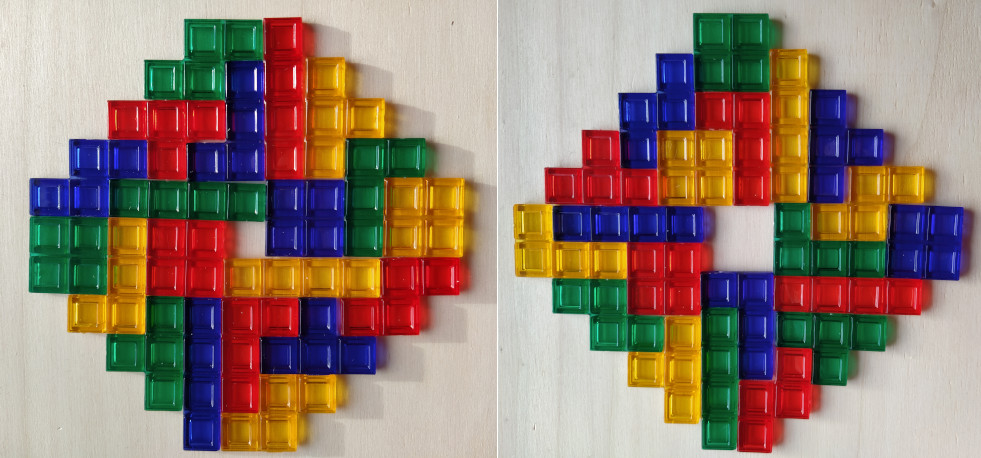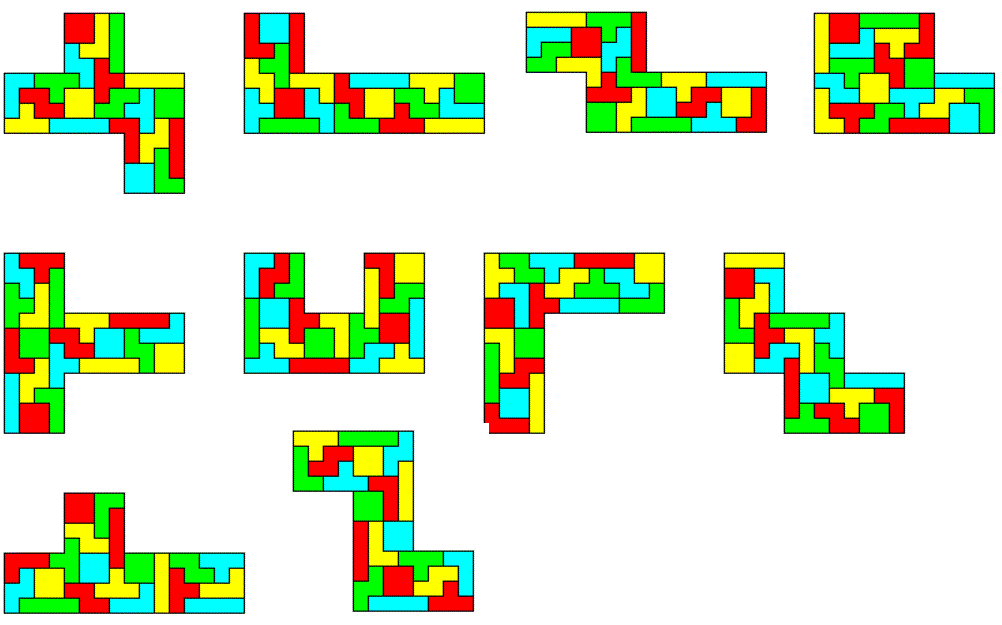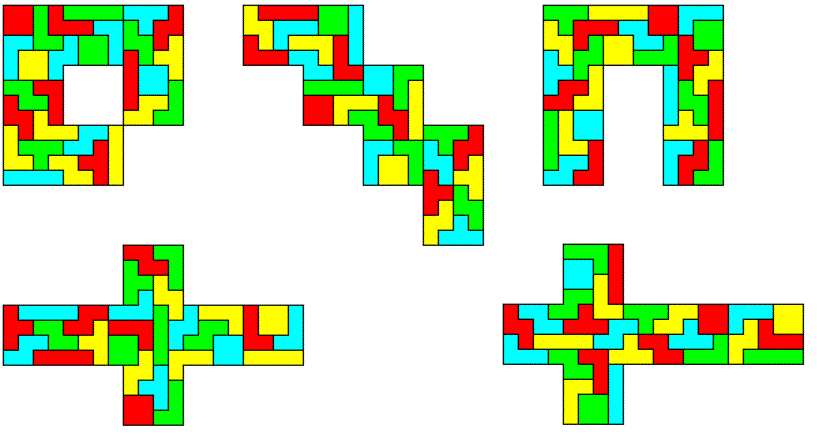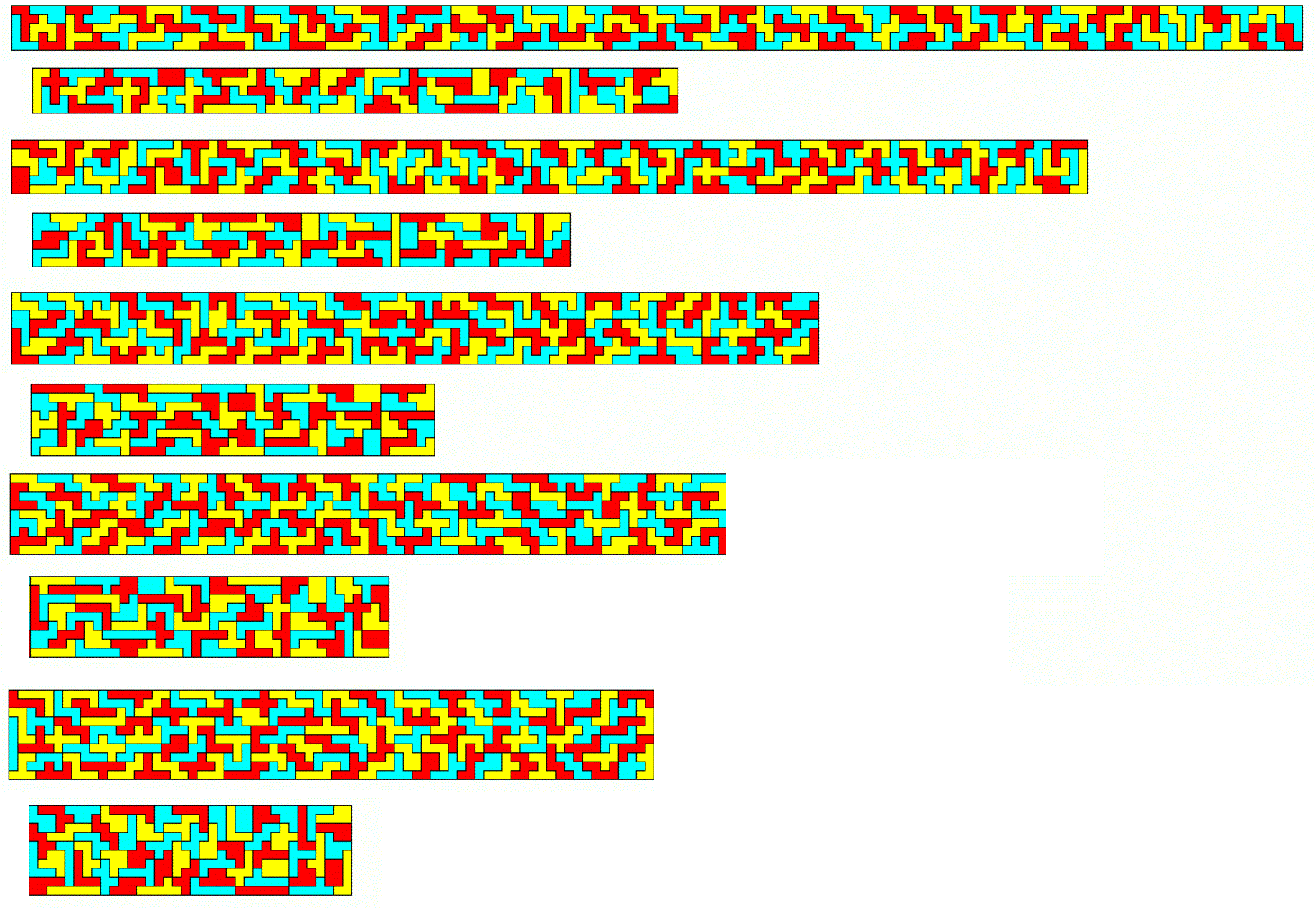Sets of Colored Polyominoes

2024/04/30
Tetrominoes are four squares connected at one or more sides. There are only five two-sided and seven one-sided tetrominoes and in these sets there is one piece, which unbalanced under checkerboard coloring. Therefore the number of nice possible constructions with these pieces is very limited. Jared McComb suggested that we can take four sets of these pieces and color them with four different colors. This way we get 20 or 28 pieces, respectively, and the number of unbalanced pieces is even. Now various constructions are possible. Furthermore we can add two conditions for a solution: A rectangle with four sets of two-sided tetrominoes is shown above.

A jagged square with a center hole made from three sets of two-sided pentominoes can also be made.

After this I explored three or four sets of tetrominoes, pentominoes or hexominoes. You can click the number of pieces in the table to see some constructions.

Basic Sets Number of squares Property One Set Three Sets Four Sets
Number of Pieces Total Area Number of Pieces Total Area Number of Pieces Total Area
Tetrominoes 4 Two-sided 5 20 15 60 20 80
One-sided 7 28 21 84 28 112
Pentominoes 5 Two-sided 12 60 36 180 48 240
One-sided 18 90 54 270 72 360
Hexominoes 6 Two-sided 35 210 105 630 140 840
One-sided 60 360 180 1080 240 1440

Three Sets of Tetrominoes, 15 Two-sided Pieces

The total area of the pieces is 60, but we can't construct any rectangle, because there are three unbalanced pieces in the set. I looked for a symmetric figur and got a kind of jagged trapezium. If we try to fill this figur, it's only possible to prevent touching pieces of same color or touchinng pieces of same shape. A construction with both conditions fulfilled isn't possible. At last I found two kind of pentagons with two jagged sides, which can be covered by the set with no touching pieces of same color or same shape.

Three Sets of Tetrominoes, 21 One-sided Pieces

Three unbalanced pieces prevent the construction of rectangles of area 84. But at least a symmetric trapezium can be made.

Four Sets of Tetrominoes, 20 Two-sided Pieces

Since the number of unbalanced pieces is even (4 T-tetrominoes), we can look for rectangles of area 80. We can get rectangles of size 10x8, 16x5 and 20x4. The first one is already shown with real pieces in the title.
Other symmetric figures are also possible. I used real pieces to show jagged rings with square symmetry.
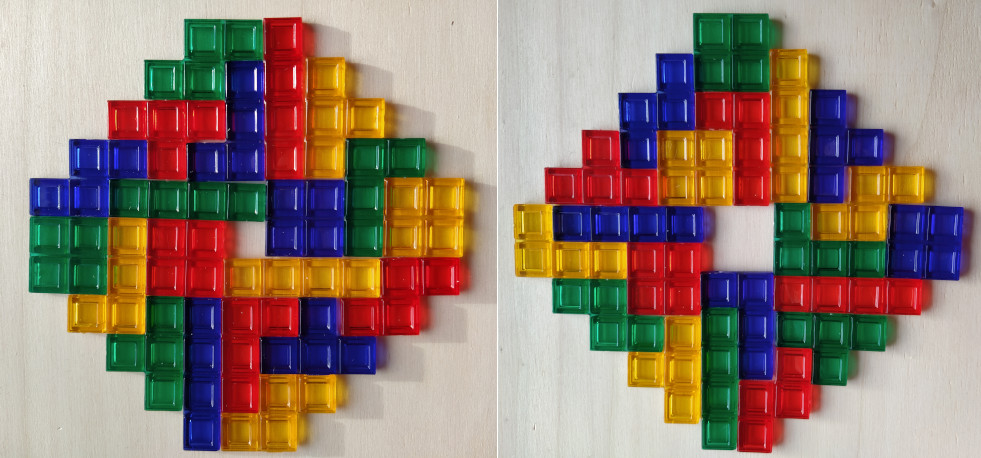A 9x9 square withh a center hole can also be made. It should also be possible to place the hole at positions with the same checkerboard coloring as the center.
What about 4-fold replicas of the pentominoes. The replica of the I-pentomino is given by the 20x4 rectangle. Ten other replicas are shown, the construction of a 4-fold X-pentomino seems to be impossible.

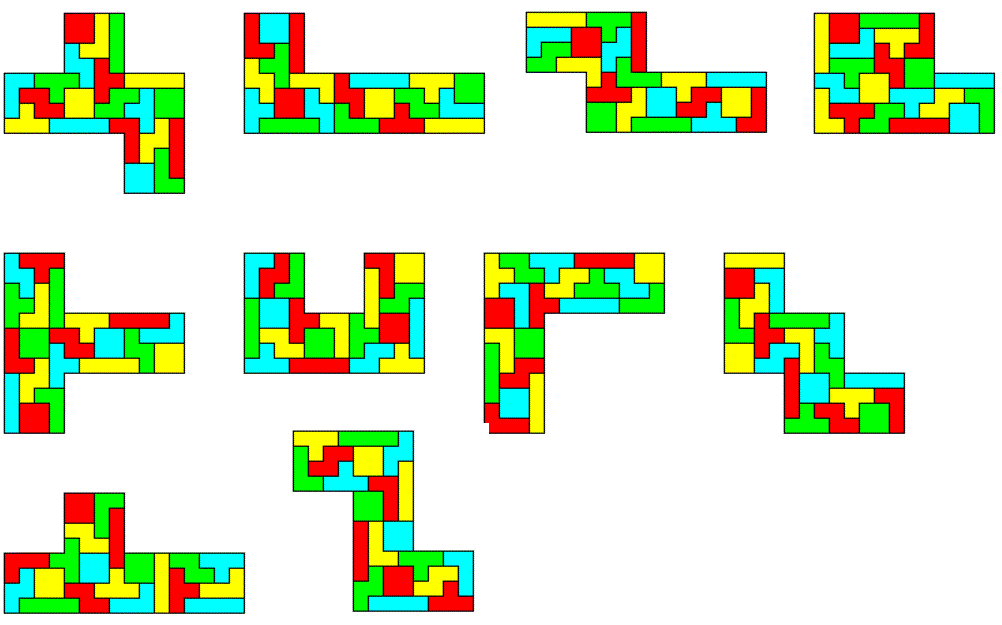
Four Sets of Tetrominoes, 28 One-sided Pieces

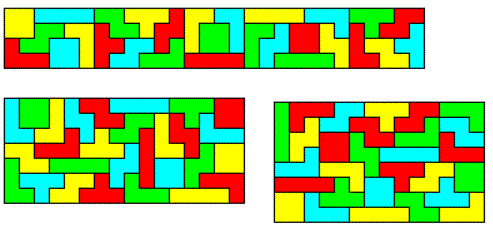
The total area of all pieces is 112. Four pieces are unbalanced, so that balanced constructions are possible. Here are the rectangles of size 28x4, 16x7, and 14x8.
Jared McComb suggested the jagged square, which was the first figure to start exploring sets of colored polyominoes.
At last we have 4-fold replicas of some heptominoes. You can split up some of these figures, put the parts together to get replicas of other heptominoes. Solutions for all heptominoes seem to possible.

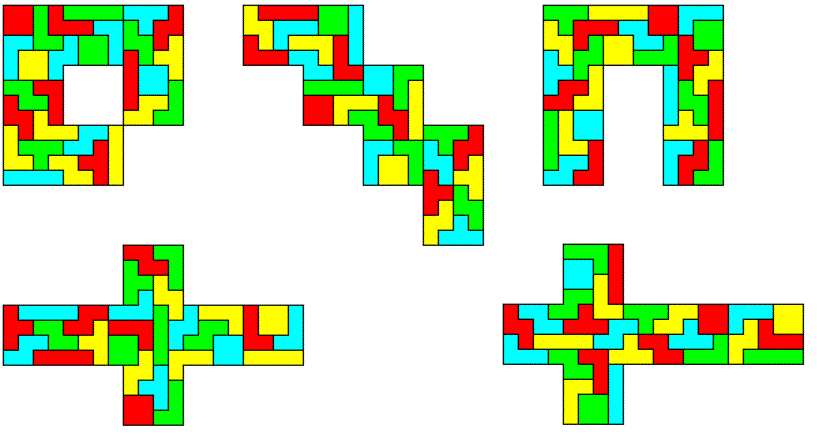
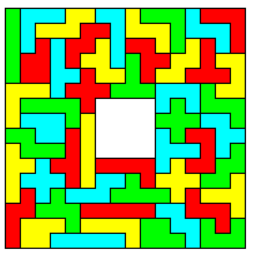
Three Sets of Pentominoes, 36 Two-sided Pieces

There are no parity problems with this set and the total of 180 allows to construct a lot of rectangles: 45x4, 36x5, 30x6, 18x10, and 15x12. I split the last rectangle into two parts of size 15x6, because backtracking on stripes is much faster.
For the 60x3 rectangle a different approach was used. Since there is an almost unique solution for the 20x3 rectangle with the basic set, I colored this solution with three colors and got two other parts by a color shift. The three parts can be combined to get the final solution.
Beside the rectangles we can also construct 6-fold scale models of the pieces.
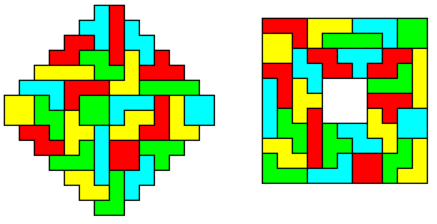
Looking for figures with square symmetry I found the jagged square of size 10 with a hole at the center. This is also shown withh real pieces below the title.
Two square rings 182-122 and 142-42 are also possible. The first one with a width of 3 was rather difficult to get, because the solution for the 20x3 rectangle wasn't useful in this case.

Three Sets of Pentominoes, 54 One-sided Pieces

The total area of the pieces is 270 .We can construct rectangles of size 90x3, 54x5, 45x6, 30x9, 27x10, and 18x15.
It seems rather difficult to construct the first rectangle as a whole figure. I used one of the few solutions for a 30x3 rectangle with the basic one-sided set, colored the solution and added two parts by a cyclic change of colors.
A jagged rectangle can also be made.

Four Sets of Pentominoes, 48 Two-sided Pieces

We have four colors and a total area of 240. So we can look for rectangles of size 60x4, 48x5, 40x6, 30x8, 24x10, 20x12, 16x15 and 80x3. Seven rectangles are shown.
The last one can be derived from 20x3 parts with three colors and a color shift for the other ones.
At last I made a square ring of size 162-42.
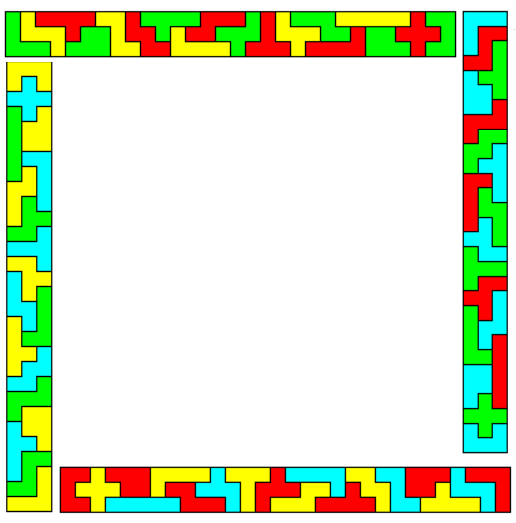
The four parts of the 80x3 rectangle can also be used for a square ring of size 232-172.

Four Sets of Pentominoes, 72 One-sided Pieces

From the 30x 3 rectangle with three colors you can get a 120x3 rectangle with four colors using a color shift.
A lot of other rectangles can be made with the set, because the total area of 240 can easily be factorized. We have rectangles of size: 90x4, 72x5, 60x6, 45x8, 40x9, 36x10, 30x12, 24x15 and 20x18.
You can also combine the four parts of the 120x3 rectangle to get a square ring.

Three Sets of Hexominoes, 105 Two-sided Pieces

Here is the set of 35 two-sided hexominoes. In this set there are 11 pieces, which are unbalanced under checkerboard coloring and they are blue marked in the picture.

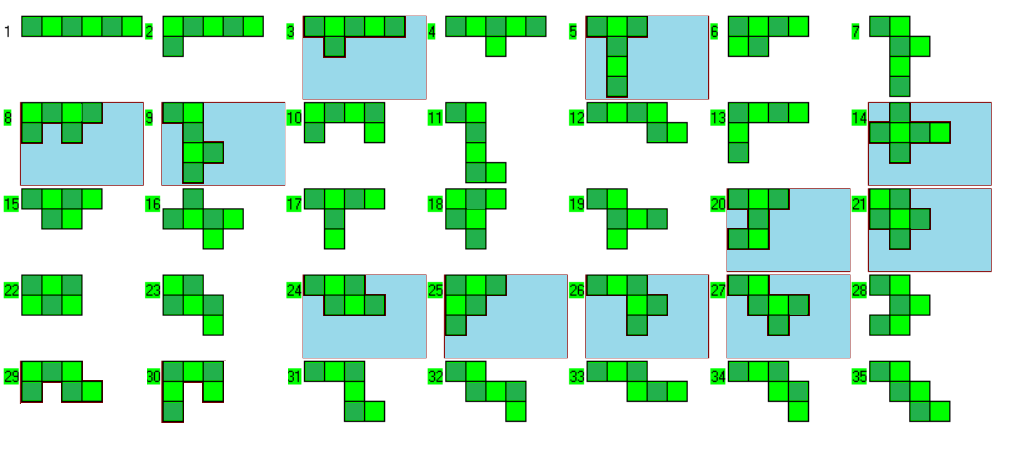
Since the total number of squares is even and the number of unbalanced pieces is odd no rectangles can be constructed with this set. The same applies to three sets of pieces, because the number of unbalanced pieces 3*11=33 is also odd. But we have a total number of 33*6*3=630 squares. This is just enough to fill a figure like a rectangular triangle with two legs of size 35 because 35*(35+1)/2=630 and the difference between white and black squares under checkerboard coloring is even.

Four Sets of Hexominoes, 140 Two-sided Pieces

We have 140 pieces with a total area of 840 and the number of unbalanced pieces is even, so there are no parity problems. A lot of rectangles can be made. If the short sides of the rectangles are smaller than 12, you can solve the figures as one part or you can split the whole figure into two parts separated by a line parallel to the short sides. Here are the solutions for rectangles of size 168x5, 140x6, 105x8, 84x10 and 70x12.

If the short sides of the rectangles are of length 12 or larger, I split the figures parallel to the long sides. Since the backtracking algorithm works column by column it is much faster for columns of low height, even if more border conditions are left for the second part. This way I got solutions for the rectangles 60x14, 56x15, and 42x20.

For the missing 35x24 and 30x28 rectangles the solutions are made from three parts.

We can also try to construct some square rings with square symmetry: 412-292, 312-112 and 292-12

At last I found a kind of jagged square.

Three Sets of Hexominoes, 180 One-sided Pieces

The total area of the 180 pieces is 1080 and the number of unbalanced pieces is even. Therefore it should be possible to construct a lot of rectangles with all pieces. But it's more difficult. If the long sides of the rectangles are above 100 the picture shows two parts of the construction. We have 216x5, 180x6,135x8, 120x9 and 108x10.

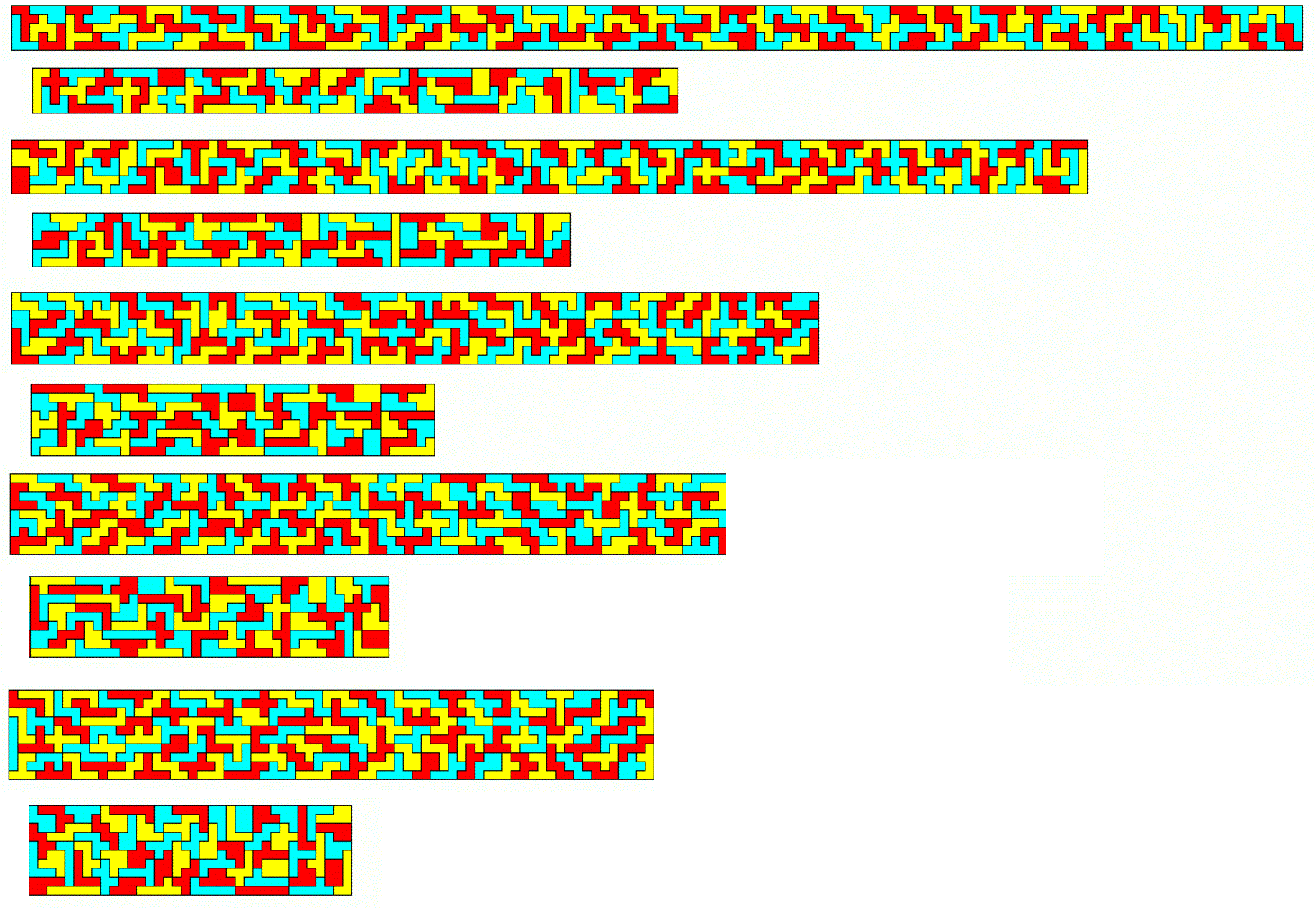
If the length of the shorter sides are above 10, you can see the horizontal dividing line. This way searching was much faster. Here are 90x12, 72x15, 60x18, 54x20, 45x24 and 36x30.

Square rings are also possible: 372-172, 512-392 and 332-32.

Four Sets of Hexominoes, 240 One-sided Pieces

We have a total of 1440 squares and no parity problems, so that a lot of rectangles can be constructed. This was a little bit easier with four colors than with three colors. But I had to adapt the search program to accept larger areas. Rectangles with shorter sides less than 12 are: 288x5, 240x6, 180x8, 160x9 and 144x10.

If the shorter sides are longer than 10 we have: 120x12, 96x15, 80x18, 72x20, 60x24, 48x30 and 40x36.

In addition I made two rings with square symmetry. The horizontal parts were filled column by column and the vertical parts row by row. 772-672 and 382-22

Home