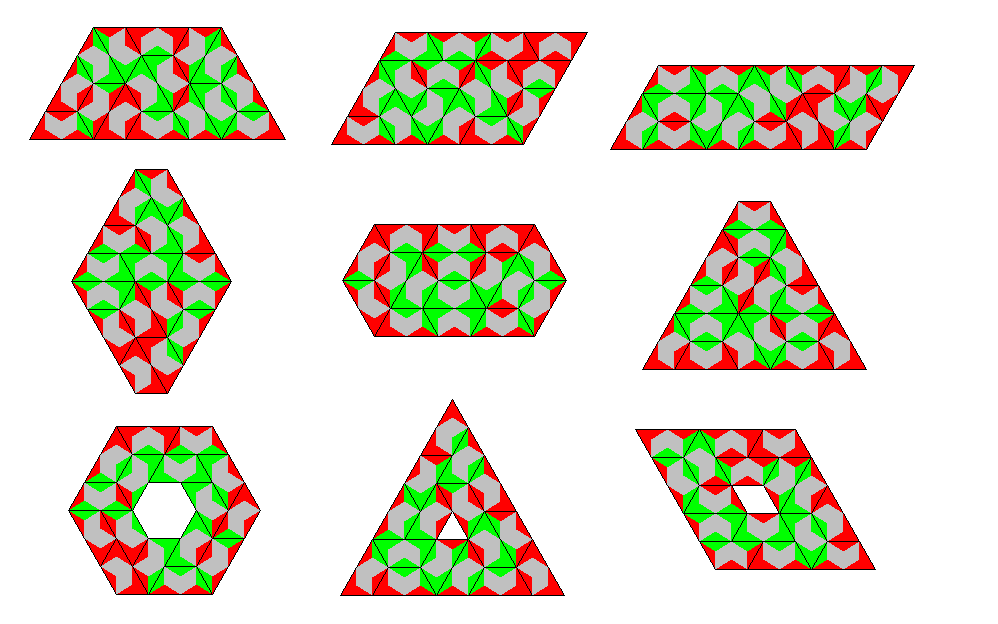Colored Triamonds

A triamond is a trapezium with a perimeter of 5 units. You can color all 5 edge units separately or you can demand the two units of the long side to be same colored. For both sets constructions are possible. Click the numbers of pieces to get the constructions.

Colors	Flip Type	Long Edge	Number of Pieces	Total Number of Triangles	Constructions
n	one-sided	split	n^5	3*n^5
	one-sided	same colored	n^4	3*n^4
	two-sided	split	(n^5+n^3)/2	3*(n^5+n^3)/2
	two-sided	same colored	(n^4+n^3)/2	3*(n^4+n^3)/2
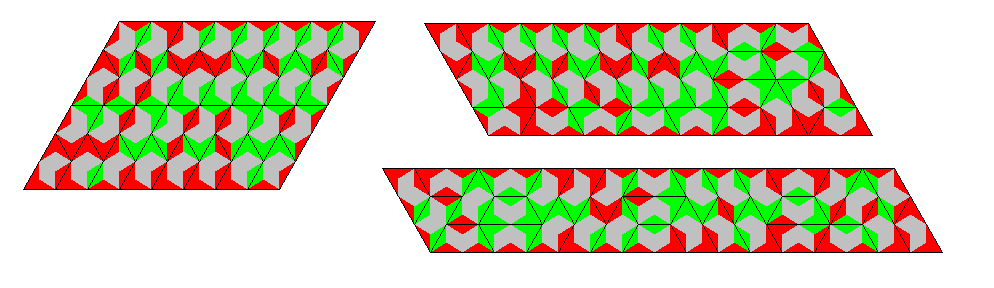
2	one-sided	split	32	96	hexagons, parallelograms, trapezes, similar hole figures, hexiamond replicas
	one-sided	same colored	16	48	hexagons, parallelograms, trapezes, similar hole figures
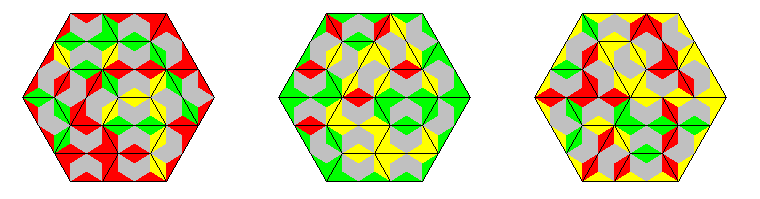
	two-sided	split	20	60	millwheel, parallelograms, trapez, similar hole triangle
	two-sided	same colored	12	36	triangle, parallelogram, ring
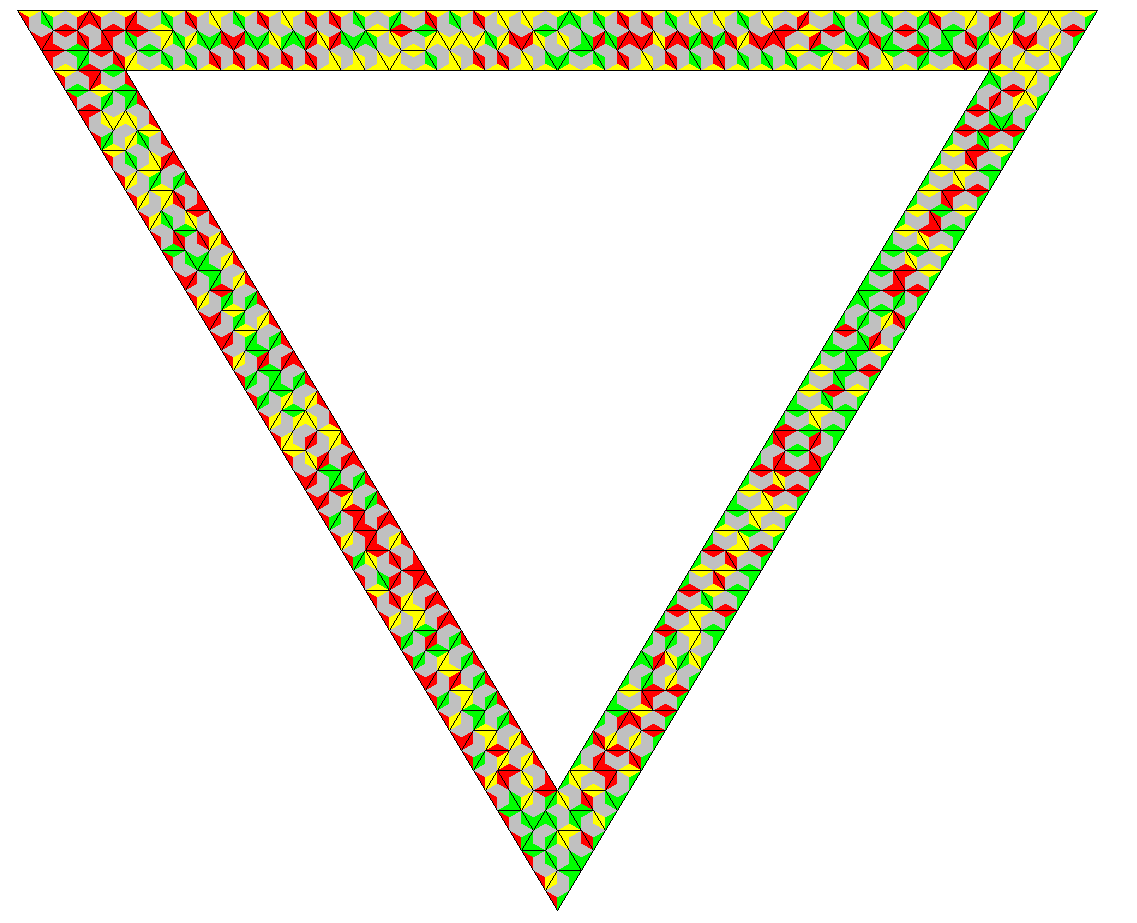
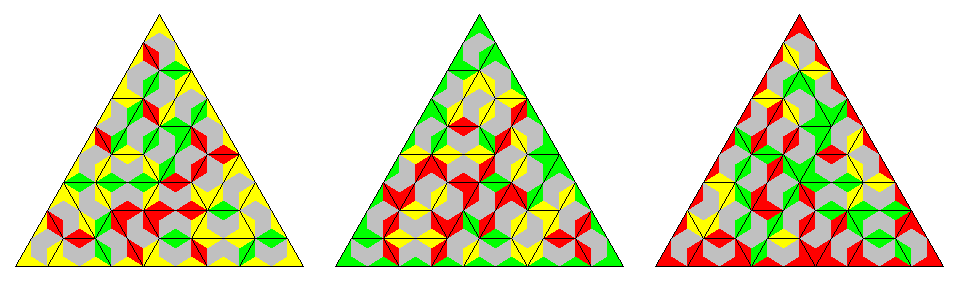
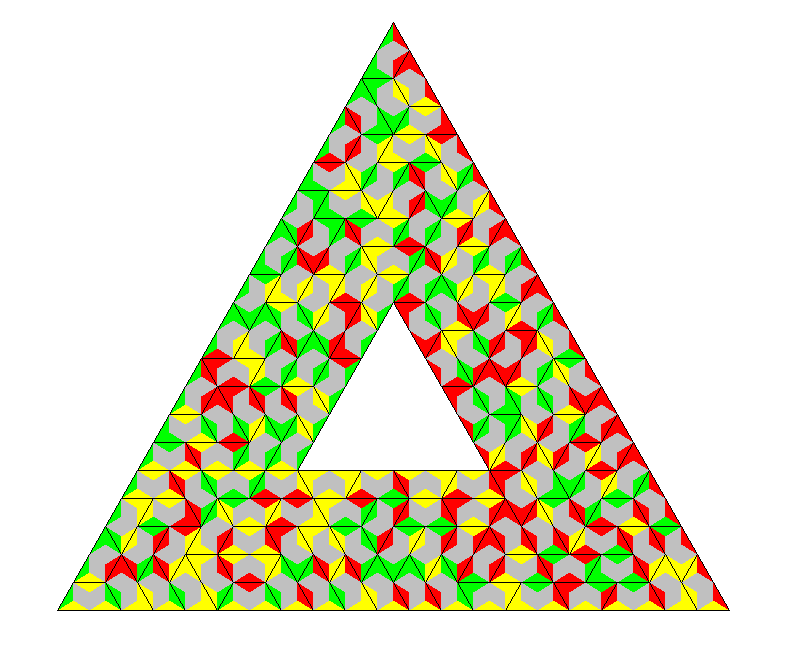
3	one-sided	split	243	729	triangle of size 27, triangle ring
	one-sided	same colored	81	243	multiple triangles of size 7
	two-sided	split	135	405	triangle ring
	two-sided	same colored	54	162	rhomb, multiple hexagons, replicas of trihexes

Two Colors, one-sided, long side split

Here are the 32 pieces made from hard foam. For one color blue triangles are stuck to the edge units for the other color the edge units are left white. The pieces look like notched triamonds with 0 to 5 notches.

With these pieces you can make a regular hexagon and some other hexagons with two axis of symmetry.

Parallelograms and trapezes can also be constructed.

Among similar hole figures is the hexagonal ring. In this case the border color of the hole and of the hexagon are different.

At last I made replicas of the 12 hexiamonds. The constructions for the parallelogram and the hexagon are already shown, the others are here.

From the crown I took a picture using the physical pieces.

Two Colors, one-sided, long side same colored

Only half of the one-sided pieces have a same colored long edge and therefore we get 16 pieces.

For instance we can make a 4-fold replica of the triamond.

Other symmetric figures are also possible.

Two Colors, two-sided, long side split

There are 20 pieces with a total area of 60 triangles. 60 is a multiple of 6 and we can get a figure, which is symmetric under 60 degree rotation. It looks like a kind of millwheel.

Some other constructions are shown below.

Two Colors, two-sided, long side same colored

Since there are 12 pieces the total area is 36 triangles, just the right number to fit the pieces into a triangle with side length 6. A 3x6 parallelogram and a semiregular hexagonal ring can also be made.

Three Colors, one-sided, long side split

There are 243 pieces and 243*5=1215 edge units with 1215/3=405 edge units per color. This is an odd number and the edges can only match if an odd number of edges of each color is placed at the border of a figure. Therefore I constructed a triangle of size 27 with each side differently colored and composed of three trapezes.

A triangle ring with an outer border of length 3*45 and an inner border of 3*36 meets the condition, too.

Three Colors, one-sided, long side same colored

Only a third of the one-sided pieces have a same colored long edge, and with 81 pieces we get 81*5/3=135 edge units of same color. This is odd again and we get the same problem as above. Three triangles of size 9 with a total perimeter of 27 for each one can be constructed, if each triangle gets a different color at the border.

Three Colors, two-sided, long side split

There are 135 pieces with 135*5/3=225 edge units of each color. Therefore an odd number of same colored edge units must be at the border. A triangle ring composed of three trapezes meets the condition.

Three Colors, two-sided, long side same colored

We have oly 54 pieces with a total area of 54*3=162 unit triangles. This allows for a 9x9 rhombus with uniformly colored border.

Multiple constructions of hexagons can also be done.

If the hexagons are colored differently at the border we can construct replicas of th trihexes.

Back
Home