Squares

If you color squares with n colors at the four sides you get (n^4+n^2+2n)/4 one-sided and (n^4+2n^3+3n^2+2n)/8 two-sided distinct pieces.

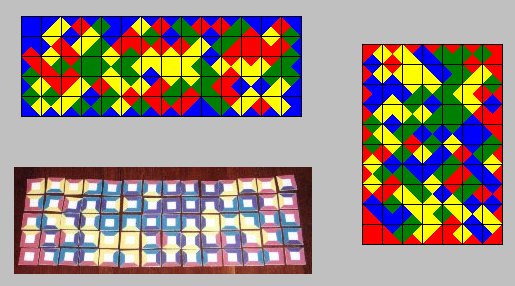
Colors	One-sided Pieces		Two-sided Pieces
	Number	Examples	Number	Examples
3	24	6x4 rectangle	21
4	70	10x7 rectangle, 14x7 rectangle	55	5x11 rectangle
5	165	15x11, 33x5 rectangles, notched square	120	12x10 rectangle
6	336	21x16, 48x7 rectangles	231	21x11, 7x33 rectangles
7	616	44x14 rectangle	406	29x14 rectangle
8	1044	36x29 rectangle, square ring 38x38-20x20	666	Two 37x9 rectangles

Only one construction with seven different edges types (406 pieces in a 29x14 rectangle) is shown, other ones can be found at Andrew Clarke's site.

For the green marked entries I produced physical pieces and additional constructions are shown.

3 colors, 24 one-sided pieces:

If yellow and green should match, the puzzle is also solvable. In this case it's equivalent to a puzzle with three different edge types (red=straight, green =male, yellow=female). A nice version with three different edge types and 12 addional copies of some pieces giving a 6x6 square is sold by Gamepuzzles.

4 colors, 70 one-sided pieces:

With some patience you can make a 10x7 and a 14x5 rectangle. I have solved both puzzles manually, but it took me a couple of hours. For a computer program it's rather easy.
If you don't bother to create the pieces yourself you can get perfect ones with different edge types or different colors from Gamepuzzles.

4 colors, 55 two-sided pieces:

There are 55 edges of same color. Therefore it isn't possible to get all edges matched. If each border of a 5x11 rectangle has a different color, the number of remaining edges of same color is even and a construction can be made.

5 colors, 165 one-sided pieces:

5 colors, 120 two-sided pieces:

6 colors, 336 one-sided pieces:

6 colors, 231 two-sided pieces:

7 colors, 616 one-sided pieces:

The last part of the construction is at the right border and a lot of pieces with the border color must be saved for the endgame. For one sided pieces this strategy worked, but for the two sided I got some problems.

7 colors, 406 two-sided pieces:

For the two sided pieces the area for the endgame is a square in the right part of the construction not touching the border. Pieces with two or more red, dark green or yellow edges are used first, then pieces with at least one edge of the mentioned colors are preferred and for the last part of the puzzle only few pieces with these "bad" colors. are left.

7 different edge types, 406 two-sided pieces:

With different edge types the construction is a bit easier and the endgame can be done at the border.

8 colors, 1044 one-sided pieces:

8 colors, 666 two-sided pieces:

There are 666*4/8=333 edges of same color. Therefore it isn't possible to get all edges matched. If each border of two 37x9 rectangle has a different color, the number of remaining edges of same color is even and a construction can be made.