Rhombs

If you color rhombs with n colors at the four sides you get (n^4+n^2)/2 one-sided and (n^4+3n^2)/4 two-sided distinct pieces.

Colors	One-sided Pieces		Two-sided Pieces
	Number	Examples	Number	Examples
3	45	9x5 parallelogram	27	three 3x3 rhombs
4	136	17x8 parallelogram	76
5	325	25x13 parallelogram	175	seven 5x5 rhombs
6	666	37x18 parallelogram	351
7	1225	35x35 rhomb	637

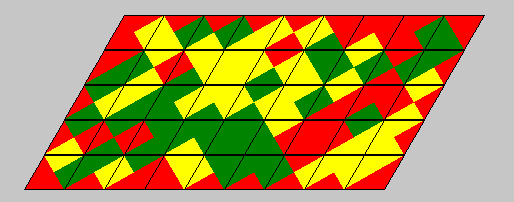
3 colors, 45 one-sided pieces:

3 colors, 27 two-sided pieces:

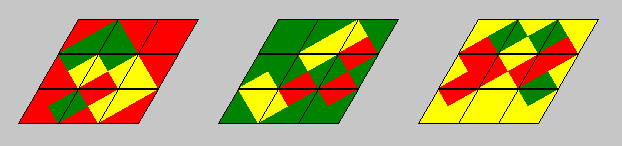
Turning the rhombs and choosing matching colors for the borders we get a hexagon. Instead of colors we can also choose straight, male and femal borders.

4 colors, 136 one-sided pieces:

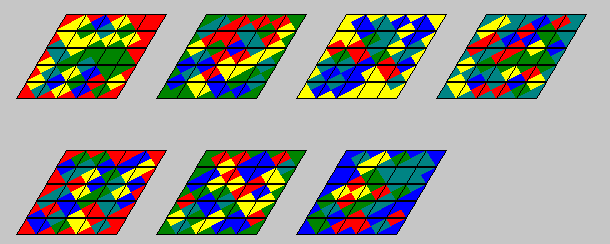
5 colors, 325 one-sided pieces:

The picture shows the method for the construction. Save all pieces with only green, teal, blue and yellow edges for the second part of the construction. A few pieces with one wrong color as the two pieces with one red edge are allowed, too.

5 colors, 175 two-sided pieces:

Since there are only five colors two couples of rhombs must get the same edge color.

6 colors, 666 one-sided pieces:

7 colors, 1225 one-sided pieces: