Isosceles Rectangular Pieces

If you color isosceles rectangular triangles with n colors at the three sides you get n^3 one-sided and (n^3+n^2)/2 two-sided distinct pieces.
With a complete set of one-sided pieces it seems to be possible to construct n congruent triangles with n^2 tiles, where each triangle has a different border color. For n=2, 5, 6 the constructions are shown below, for n=8 look at the title and for n=1, 3, 4, 7 the construction is possible as well. So far I haven't seen a solution for n>8. Would you like to write your own program to get a solution? May be there is a systematic approach for a construction.

Various rectangles, triangles and replicas of polyabolos can be found. If the number of long sides with same color is odd, these edges can't match and you have to look for multiple figures as shown above or you can choose pairs of different edge types (silver marked) instead of edge colors (yellow marked). With such pieces n-fold replicas of n-abolos or n-tans may be possible even if n is odd.

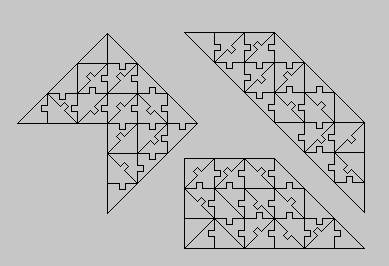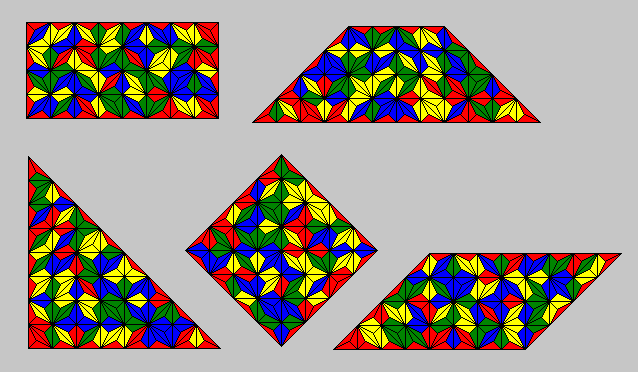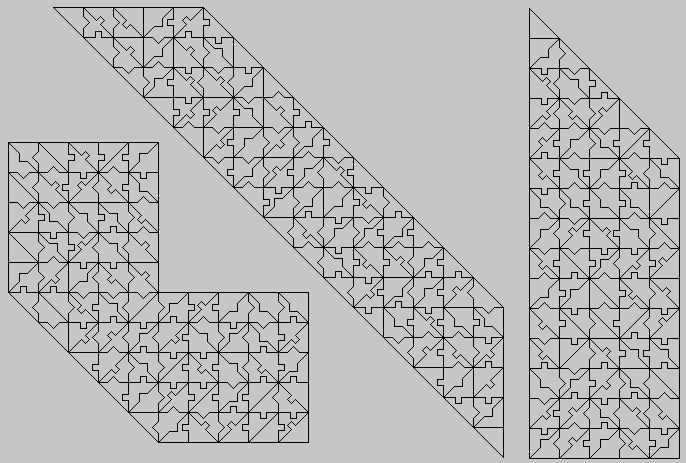
Colors	One-sided Pieces		Two-sided Pieces
	Number	Examples	Number	Examples
2	8	2x2 square	6
3	27	3-fold replicas of triabolos	18	see online puzzle
4	64	8x4 rectangle, 4sqrt(2)x4sqrt(2) square, size 8 triangle, other 4-fold replicas of tetrabolos	40	4x5 rectangle
5	125	5-fold replicas of pentabolos	75	5-fold replicas of triabolos
6	216	hexabolo star	126
7	343		196	7sqrt(2)x7sqrt(2) square, size 14 triangle
8	512	16x16 square	288	12x12 square