Cubes with 4 Colors
240 is a nice number to factorize and therefore we can try for a lot of boxes.
First I constructed boxes with opposite faces same colored and got
the 4x4x15 box ( see layers ) and
two 4x5x6 boxes ( see layers ),
which can be combined to 4x6x10, 5x6x8 and 4x5x12 boxes. The 3x4x20 box seems to be difficult, may be
even impossible, since 2x4x20 = 160 cubes with one common color at one face are needed and only 240 - 57 = 183
are available.
What's worse, some of these cubes need another cube of the common color to get a matching neighbour.
For the 4x4x15 box( see layers )
and the 5x6x8 box ( see layers )
I found also constructions with checkerboard coloring outside.
This should be possible for the other boxes, too.
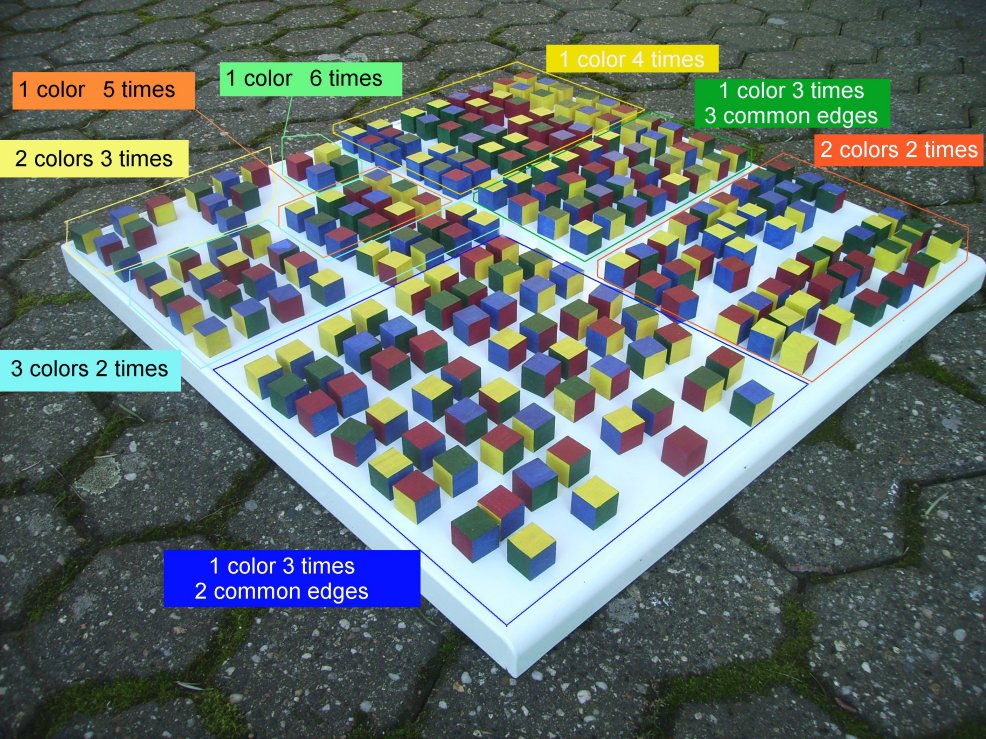
I wanted to make a real construction with the help of the computer solution. Searching for the
matching cubes in a set of 240 is rather difficult. Therefore I made subsets of the cubes
according to the frequencies of colors on them. The distribution of the most frequent color on the cube faces
was a second hint to find the right cube more easily. The dissection of the whole set is shown above.

You can also try to replicate the pentominoes 4 times as large in x and y direction and 3 times as large in height.
For bottom and top I chose two different colors due to the problems discussed in connection with the 4x20x3 box,
but the other pairs of opposite faces got the same colors. The replicas of the U, Z, L, N, Y, F and P pentominoes are combinations
of a 4x8x3 box and a replica of the L-tromino ( see layers ), the T and V pentominoes are made
of a 4x8x3 box and a 4x12 box ( see layers ).
For the I and X pentomino I used a special construction.


Index
Home




