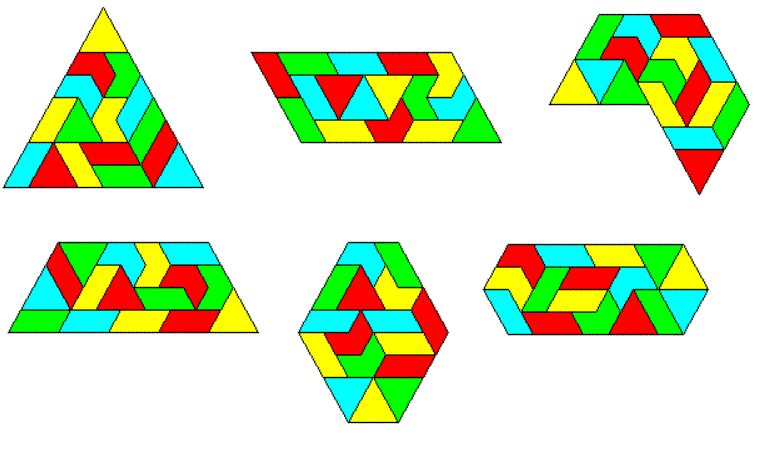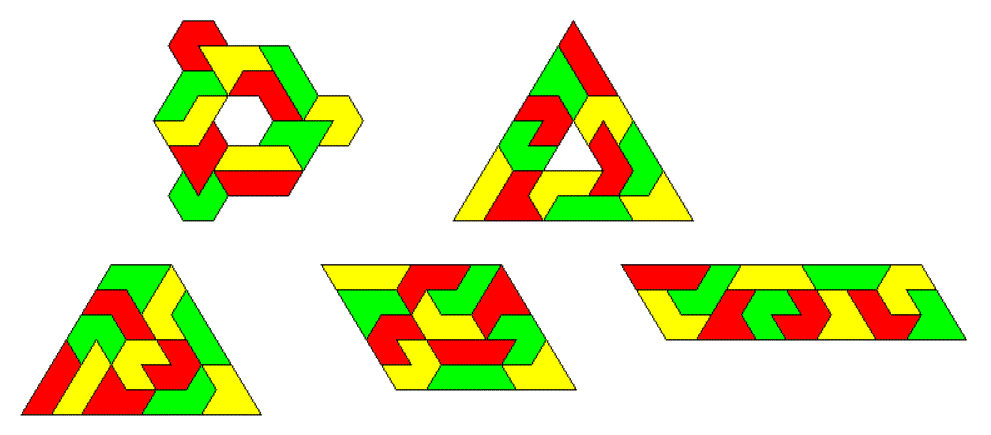Tetriamonds
With the following SVG file you can easily cut or print the 3 tetriamonds. To get the set of one-sided pieces you must additionally reflect the first piece. Then we have 1*2+2 = 4 one-sided pieces.

Three Sets of Two-sided Tetriamonds
There are 3*3=9 pieces with a total of 36 triangles.
Two pieces among the three simple tetriamonds are balanced under checkerboard coloring. Only the triangle is a unbalanced one. Therefore three sets of triamonds can only cover a figure, which is unbalanced like a triangle with side length of six units.

Here are three other figures, which are also unbalanced and they can easily be solved by hand.
The solutions are here.
Four Sets of Two-sided Tetriamonds
There are 4*3=12 pieces with a total of 48 triangles.
Four sets of tetriamonds have four unbalanced pieces and therefore balanced figures like the following one can be constructed.

Here are some other symmetric figures and their solutions. The hole in the triangles of size 6 cannot be placed at the center or at the corner, because the figures aren't balanced in that case.
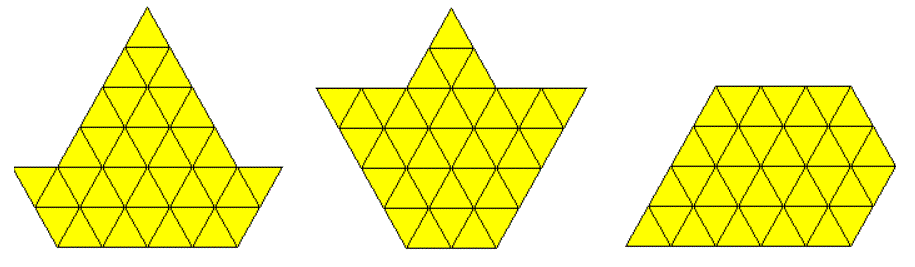
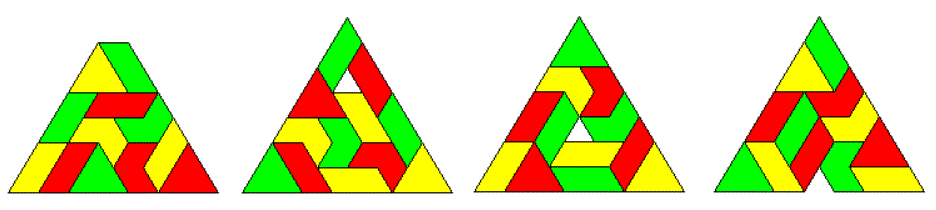
Three Sets of One-sided Tetriamonds
There are 3*4=12 pieces with a total of 48 triangles.
The total number of triangles in this set is the same number of triangles as the number of triangles in the four colored sets of two-sided tetriamonds. But now the total set is unbalanced and all figures of the last set cannot be constructed. Otherwise a triangle of size 6 with a center hole or with a missing corner are possible to make.
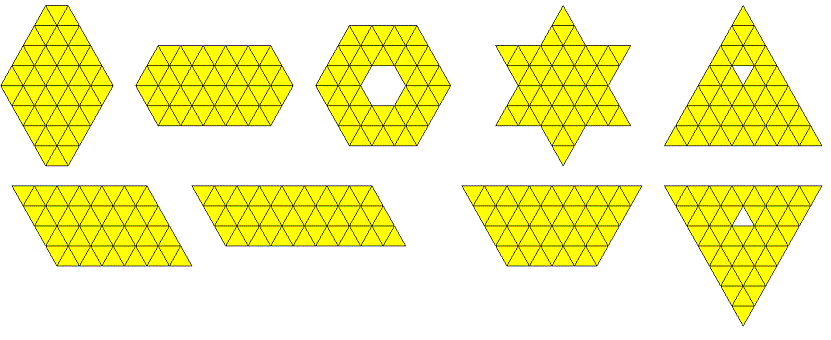
Four Sets of One-sided Tetriamonds
There are 4*4=16 pieces with a total of 64 triangles.
With four unbalanced pieces we can construct balanced figures. The triangle of size 8 is a 4-fold replica of the triagonal tetriamond. For the other triamonds we can also get 4-fold replicas. Furthermoer a trapezium and symmetric hexagons are possible.
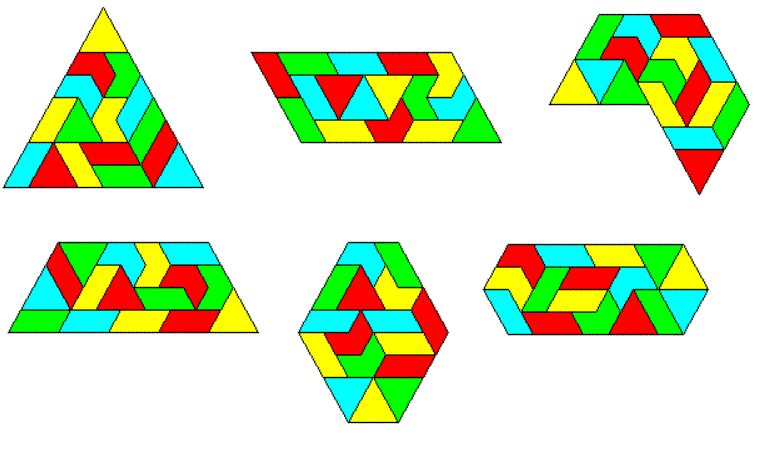
Pentiamonds
With the following SVG file you can easily cut or print the 4 pentiamonds. To get the set of one-sided pieces you must reflect all pieces with exception of the 2 symmetric ones. Then we have (4-2)*2+2 = 6 one-sided pieces.

Three Sets of Two-sidedPentiamonds
There are 3*4=12 pieces with a total of 60 triangles.This number of triangles is suitable for constructions with rotational symmetry.

Symmetry under 120° rotation, a trapezium and parallelograms of size 19x3 and 6x5 are also possible.
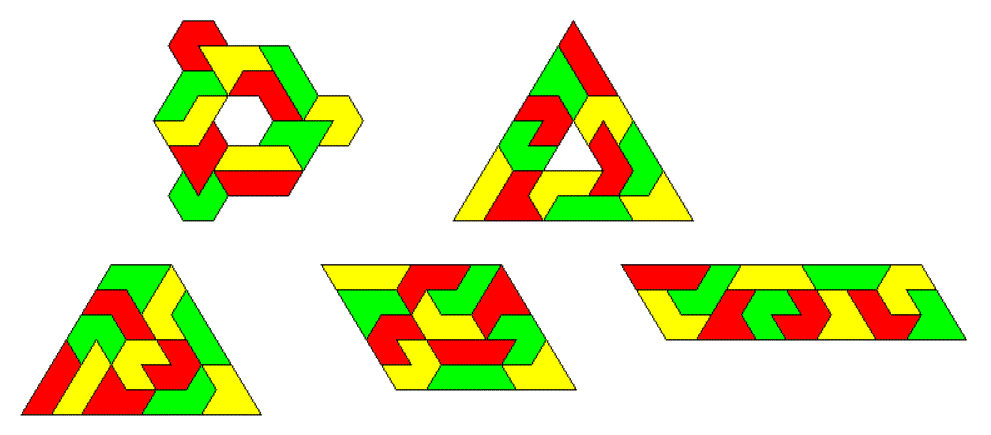
Four Sets of Two-sided Pentiamonds
There are 4*4=16 pieces with a total of 80 triangles. Here is an example with real pieces.

With a total of 80 triangles you can't get figures, which are symmetric under 60° or 120° rotation. But parallelograms of size 8x5, 10x4 or even 20x2, which are symmetric under 180° rotation can be made. A lot of figures with mirror symmetry are possible as well.
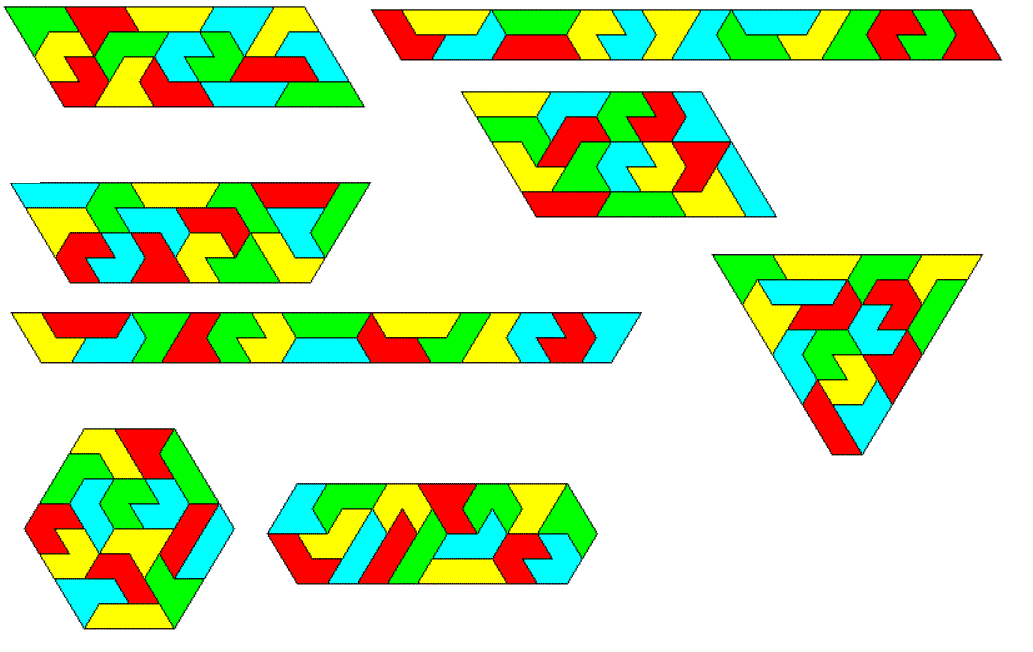
Three Sets of One-sided Pentiamonds
There are 3*6=18 pieces with a total of 90 triangles.
Since 90=2*45 and 45=3*3*5 we can only construct two parallelograms of size 9x5 and 15x3. A hexagonal ring and a mirror symmetric hexagon are also possible.
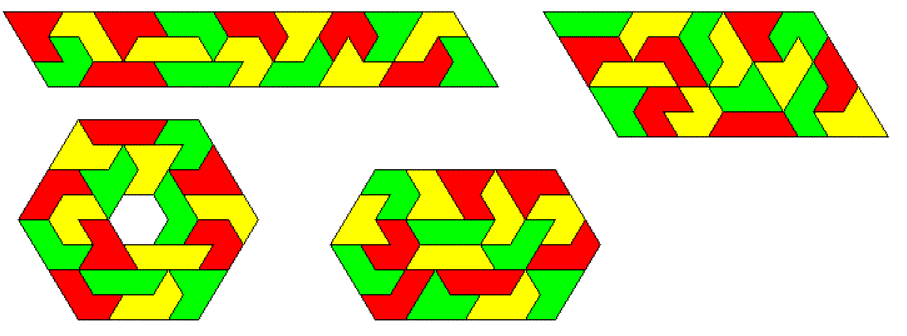
Four Sets of One-sided Pentiamonds
There are 4*6=24 pieces with a total of 120 triangles.
Therefore we can make many parallelograms: 30x2, 20x3, 15x4, 12x5 and 10x6. I added a hexagon of size 6 with a hexagoanl hole of size 4.
Hexiamonds
With the following SVG file you can easily cut or print the 12 hexiamonds. To get the set of one-sided pieces you must reflect all pieces with exception of the 5 symmetric ones. Then we have (12-5)*2+5 = 19 one-sided pieces.

Three Sets of Two-sided Hexiamonds
There are 3*12=36 pieces with a total of 216 triangles. If we start with a ring of size 6 and a hole of size 2, we can add 6 triangles of size 2 to get a star like figure with rotational symmetry.

Parallelograms and convex, symmetric figures with 5 or 6 corners are also possible. The regular hexagon is here.

Four Sets of Two-sided Hexiamonds
There are 4*12=48 pieces with a total of 288 triangles. As usual we can look for parallelograms of size 48x3, 36x4, 24x6, 18x8 and 16x9.

Since 288 is a multiple of 6, I constructed two figures with rotational symmetry and added the triangle of size 17 with one missing corner.

Three Sets of One-sided Hexiamonds
There are 3*19=57 pieces with a total of 342 triangles. I took a hexagon of size 7 with 294 triangles and added 8 triangles at each corner.

Since 342/2=171=19*9 , the pieces can cover a parallelogram of size 19x9.

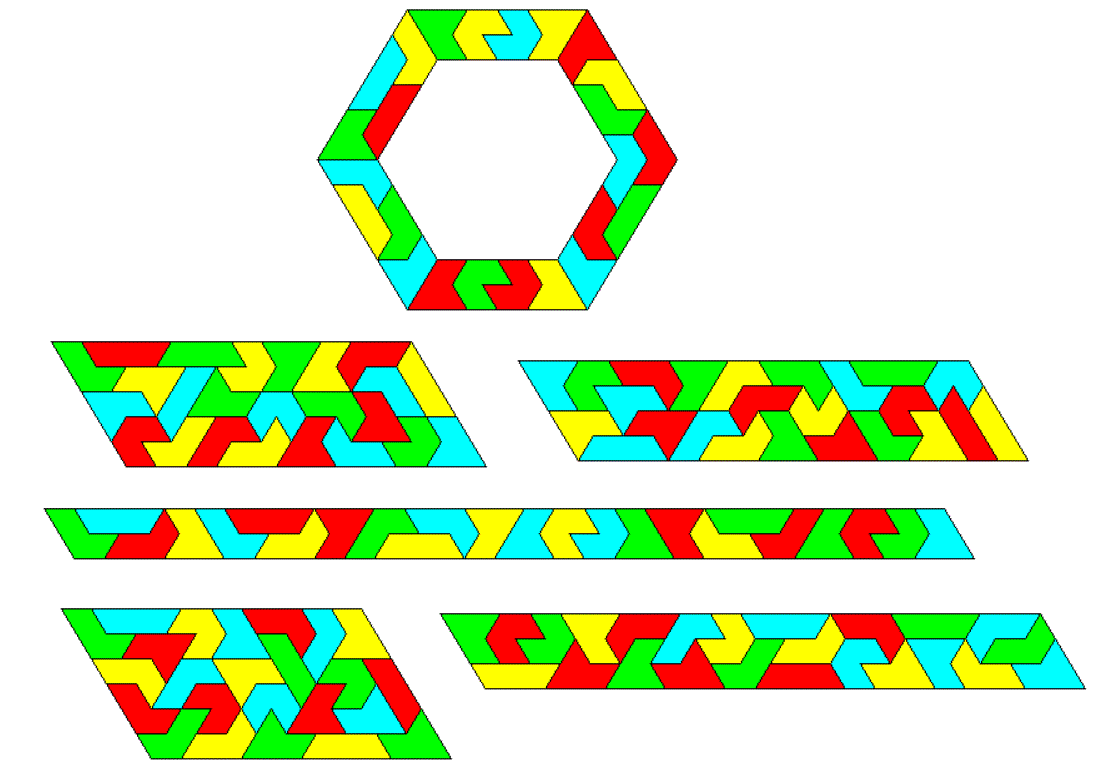
Four Sets of One-sided Hexiamonds
There are 4*19=76 pieces with a total of 456 triangles. Some figures with rotational symmetry seem to be possible to construct. One example is shown.

With four colors it isn't difficult to get parallelograms of size 57x4, 38x6 and 19x12.

Heptiamonds
With the following SVG file you can easily cut or print the 24 heptiamonds. To get the set of one-sided pieces you must reflect all pieces with exception of the 5 symmetric ones. Then we have (24-5)*2+5 = 43 one-sided pieces.

Three Sets of Two-sided Heptiamonds
There are 3*24=72 pieces with a total of 504 triangles. Since 504 mod 6 = 0, you can make figures with hexagonal symmetry.
 We have 504=2*252=2*(2*2*3*3*7) and a lot of parallelogram is possible:63x4, 42x6, 36x7, 28x9, 21x12 and 18x14.
We have 504=2*252=2*(2*2*3*3*7) and a lot of parallelogram is possible:63x4, 42x6, 36x7, 28x9, 21x12 and 18x14.

Here are some examples with mirror symmetry.

Four Sets of Two-sided Heptiamonds
There are 4*24=96 pieces with a total of 672 triangles. An example for figures with hexagonal symmetry is a hexagon of size 11 with a hexagonal hole of size 3.

Factorizing 672=2*336=2*(2*2*2*2*3*7) leads to various paralellograms: 84x4, 56x6, 48x7, 42x8, 28x12, 24x14 and 21x16.

Three Sets of One-sided Heptiamonds
There are 3*43=129 pieces with a total of 903 triangles. Since 903 isn't a multiple of six and even odd, figures symmetric under 60° rotation or parallelograms aren't possible. But you can get a trapezium or a figure with triangle symmetry for example.


Four Sets of One-sided Heptiamonds
There are 4*43=172 pieces with a total of 1204 triangles. Since 1204=43*4*7=2*43*2*7 we can try to construct parallelograms of size 86x7 or 43x14.

Octiamonds
With the following SVG file you can easily cut or print the 66 octiamonds. To get the set of one-sided pieces you must reflect all pieces with exception of the 12 symmetric ones. Then we have (66-12)*2+12 = 120 one-sided pieces.

Three Sets of Two-sided Octiamonds
There are 198 pieces with a total of 1584 triangles. To construct the three hexagonal rings I divided each ring into three thirds and covered the thirds with pieces so that each shape of the octiamonds was used. If one third is finished you can derive the other ones by a color shift replacing the colors 1,2,3 by 2,3,1. At the touching borders of the parts you must ensure that touching pieces differ in color.

Three parts of the parallelograms 72x4, 132x6 and 39x8 are separately shown but can be combined without color problems. For the third parallelogram I copied the begining of the second part at the end of the first part to demonstrate the different colors at the border.

The parallelograms of size 73x11 and 66x12 are short enough to show them as whole polygons. The remaining parallelograms 44x18, 36x22 and 33x24 are split parallel to their long sides getting more color constraints at their common borders.

Four Sets of Two-sided Octiamonds
There are 264 pieces with a total of 2112 triangles. We can divide a hexagonal ring of size 19 with a hexagonal hole of size 3 into four parts. But these parts aren't congruent. Therefore the color shifting method cannot be applied and we need four steps to get a solution.

What about parallelograms? We can use the solutions for parallelograms with three sets of colored octiamonds and change the color shift from (1,2,3 > 2,3,1) to (1,2,3,4 > 2,3,4,1). Only the parallelogram of size 66x16 cannot be constructed this way. I divided the whole figure into three parts.

Three Sets of One-sided Octiamonds
There are 360 pieces with a total of 2880 triangles.
Among the 120 pieces of one-sided octiamonds there are 37 pieces with a coloring excess of 2 triangles, as noticed at The PolyPages. Therefore no parallelograms can be made. This is also true for three sets of pieces because 3*37=111 is odd as well. But we can look for constructions with triangle symmetry or trapezia with one axis of symmetry.
Take a triangle with side length a and cut off or cut out a triangle of size b. If you get a trapezia, neccessary conditions are 2880=a2-b2 and (a-b ) mod 4 = 2. This is also true for a similar hole construction, if each side of the triangle hole is parallel to a side of the big triangle. If the hole is upside down the second condition changes to (a+b) mod 4 = 2.
At first I tried to get figures, which can be divided into three congruent trapezia. These trapezia can be solved by the color shift method, if the borders fit together. With side lengths 53-10-43-10 we get a triangle ring of of size 83 - 33 and a thickness of 10.

Using trapezia with side lengths 83-6-77-6 we get a triangle ring of size 89 - 71 and a width of 6.

Using trapezia with side lengths 31-30-1-30 we get a triangular similar hole figure of size 61 - 29.

Three trapezia can also be used to make longer trapezia, but it's more difficult to get different colors at the touching borders. Here are three trapezia with side lengths of 53-10-43-10. Take the first one and move it to the right end of the second one. Then take the third one and move it to the left end of the second one. This way we have a trapezium of size 139-10-149-10.

Here are three trapezia with side lengths of 83-6-77-6. Take the first one and move it to the right end of the second one. Then take the third one and move it to the left end of the second one. This way we have a trapezium of size 237-6-243-6. By the way the three trapezia can also be used to get a triangle ring like the one above.

Four Sets of One-sided Octiamonds
There are 480 pieces with a total of 3840 triangles. Since there are four sets of simple octiamonds the coloring excess is zero and parallelograms are possible to construct. Furthermore it's muchh easier to work with four colors. Two examples are shown. The first one is divided into three parts.


A ring is an example for a figure with symmetry under 60° rotation.

A rhomb of size 44x44 with a similar hole of size 4x4 has two orthogonal axes of symmetry.

Home