Here are two figures with hexagonal symmetry. The second one is a little bit harder to solve because both parts are rather thick.

The semi regular hexagon of size 12-10-12-10-12-10 has triangle symmetry without any holes.
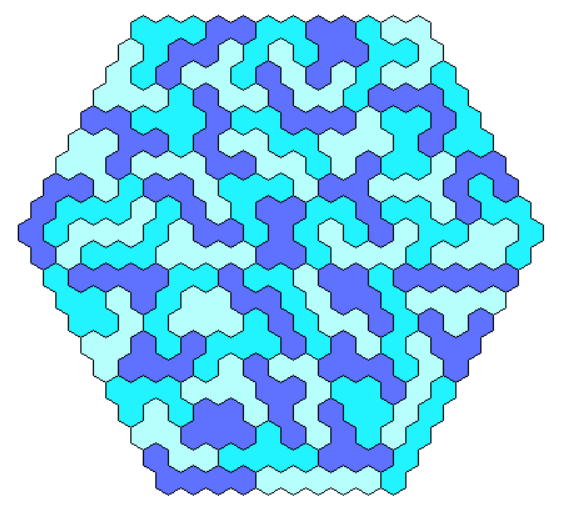
For symmetry under 180 degree rotation without axes of symmetry you can look for hexagons and parallelograms.

Since 330=2*3*5*11 a lot of parallelograms is possible to fill. Here are the solutions for 10x33, 11x30, 15x22 and 6x55.

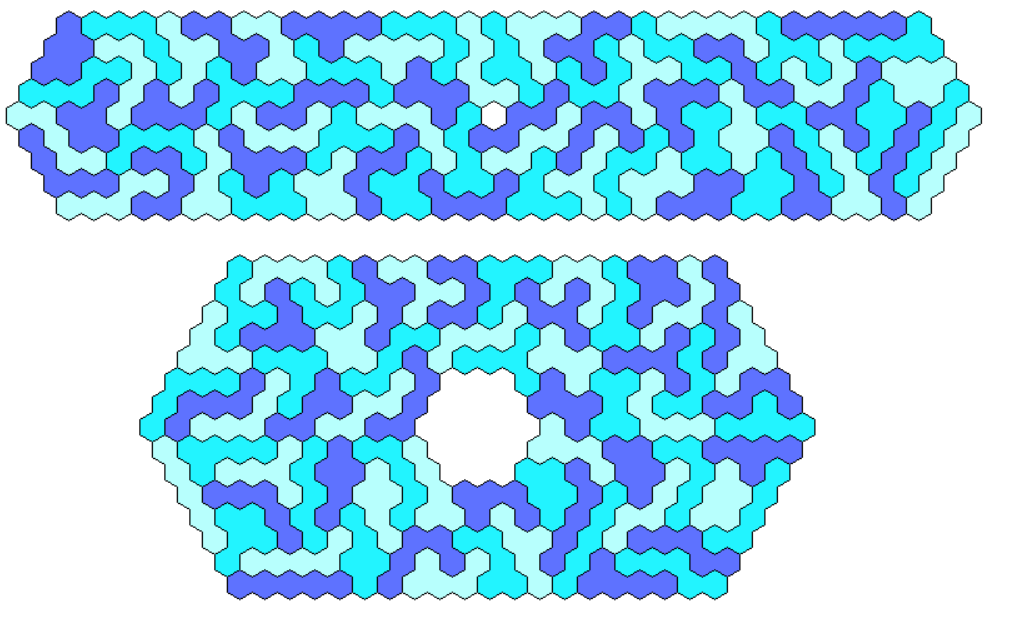
The 3x110 parallelogram is made from two parts. The first part is also used for a trapezium of height 3.

A hexagon with two axes of symmetry can be made with a hexagonal hole at the center.
Among figures with one axis of symmetry we have various trapezia of height 5, 11, 18, 15 and 20.

A trapezium of height 3 is only missing. For the first part I used the first part of the 110x3 parallelogram.

To get all convex hexagons with an area of 330 you have to solve 330*2 = g(g+1)- a(a+1) - b(b+1) - c(c+1). Among these hexagons two symmetrical ones are shown.

The 99 pieces have a total area of 495 just enough for a semi regular hexagon with triangle symmetry and no hole.
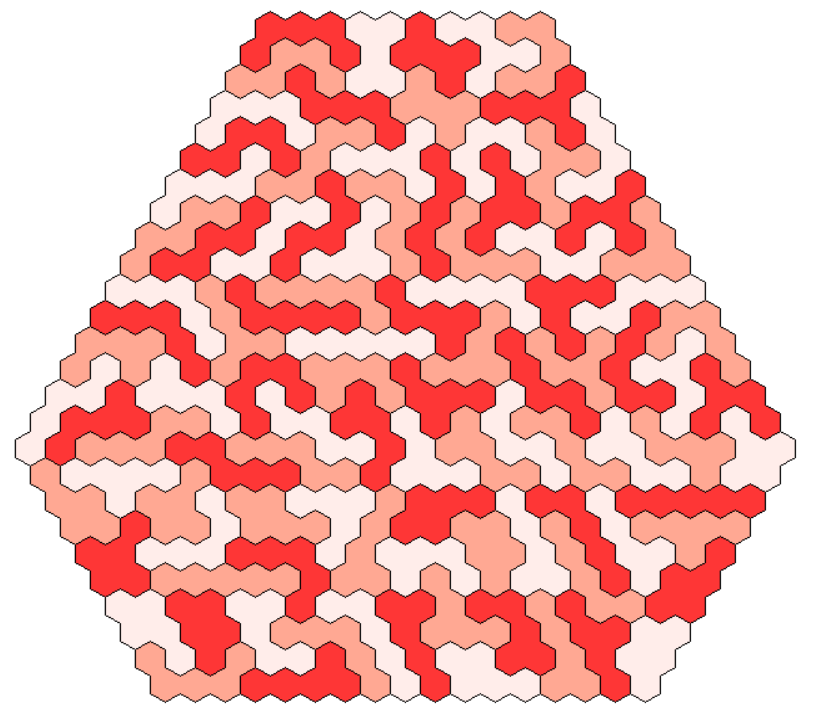
Another nice symmetric figure with triangle symmetry is a triangle of size 31 with a center hole.

A kind of rectangle can also be filled with this set.

I also tried to fill three congruent rectangular shapes.

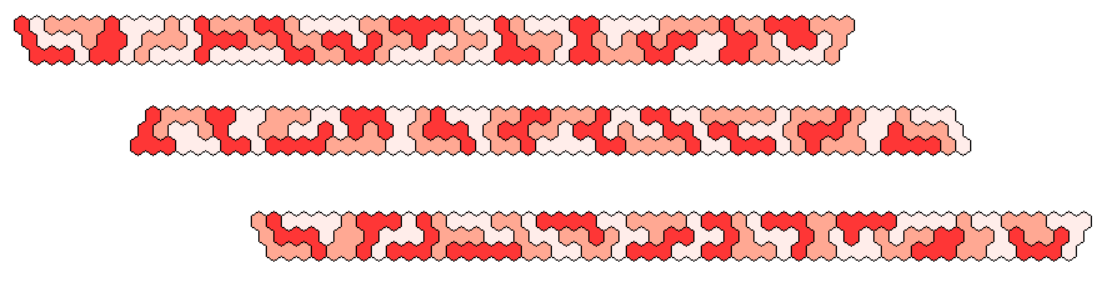
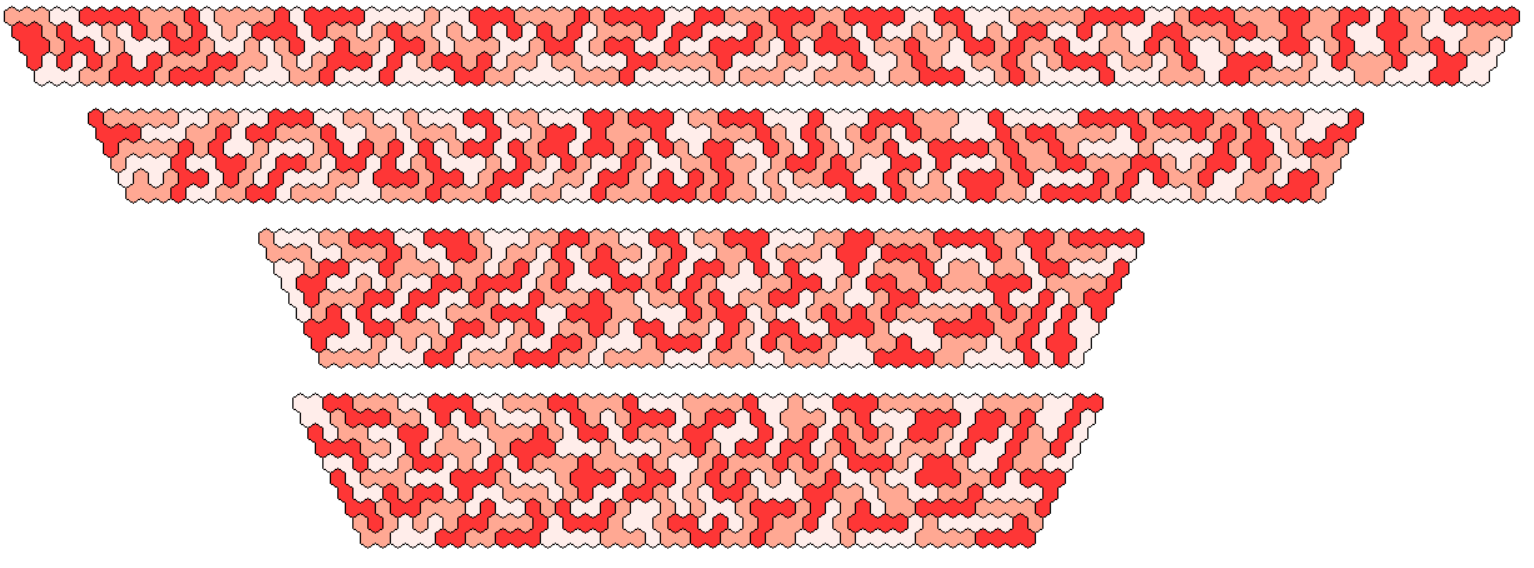
495=3*3*5*11. Therefore I looked for paralellograms of size 3x165, 5x99, 9x55, 11x45 and 15x33. The last three ones are shown at first.

The parallelograms of height 5 and 3 are made from three congruent parts of size 33x5 and 55x3, respectively. For the parallelogram of height 3 a different approach was used. One part was solved so that it contains all shapes of the pentahexes. The other two parts are given by a color shift.

Solving the equation a(a+1) - b(b+1) = 495*2, 0 < b, b < a we get trapezia of height 3, 5, 6, 8, 10, 11, 15, 18, 22 and 30.
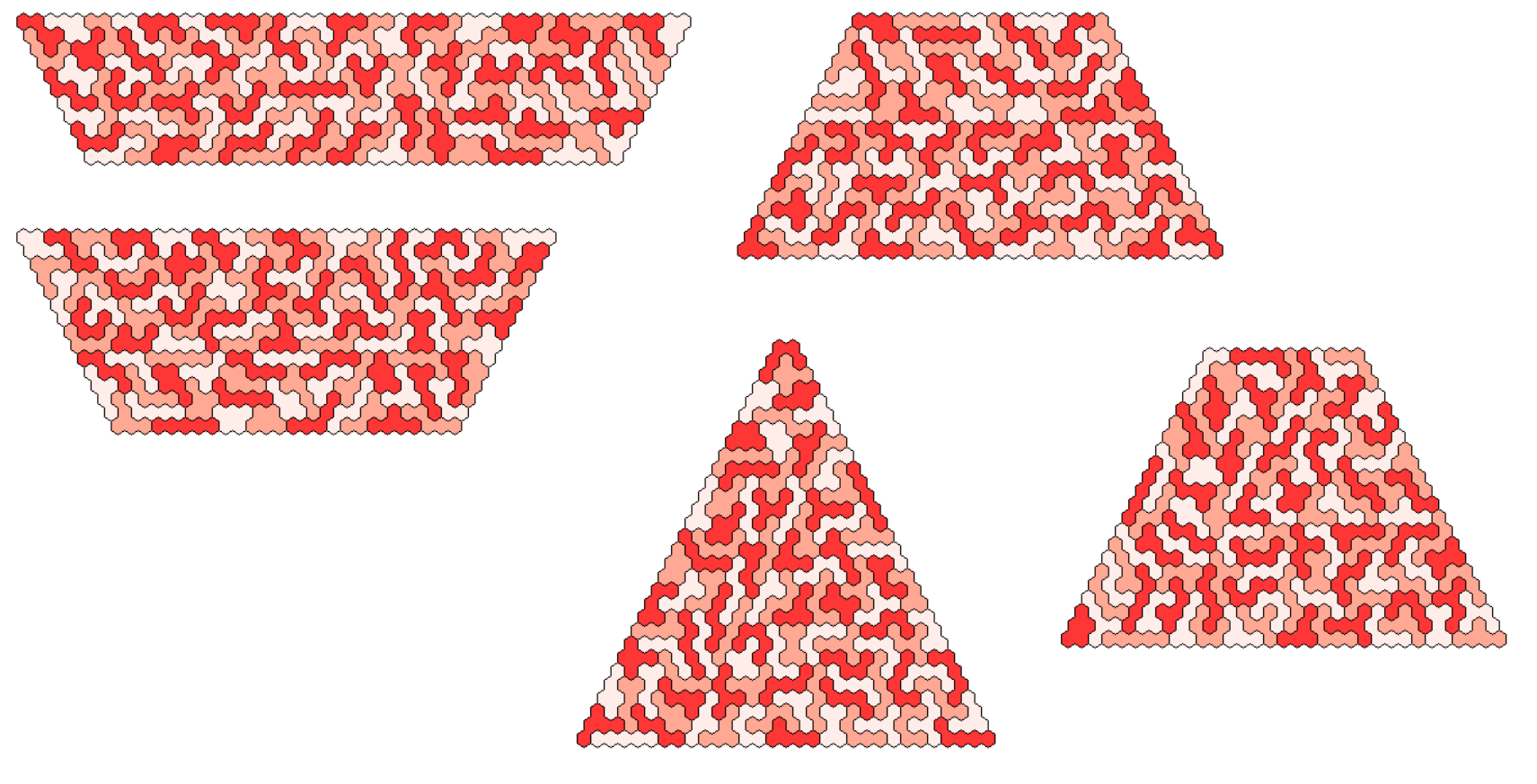
The trapezium of height 3 is solved by three congruent trapezia using the same method as described for the parallelogram of height 3.