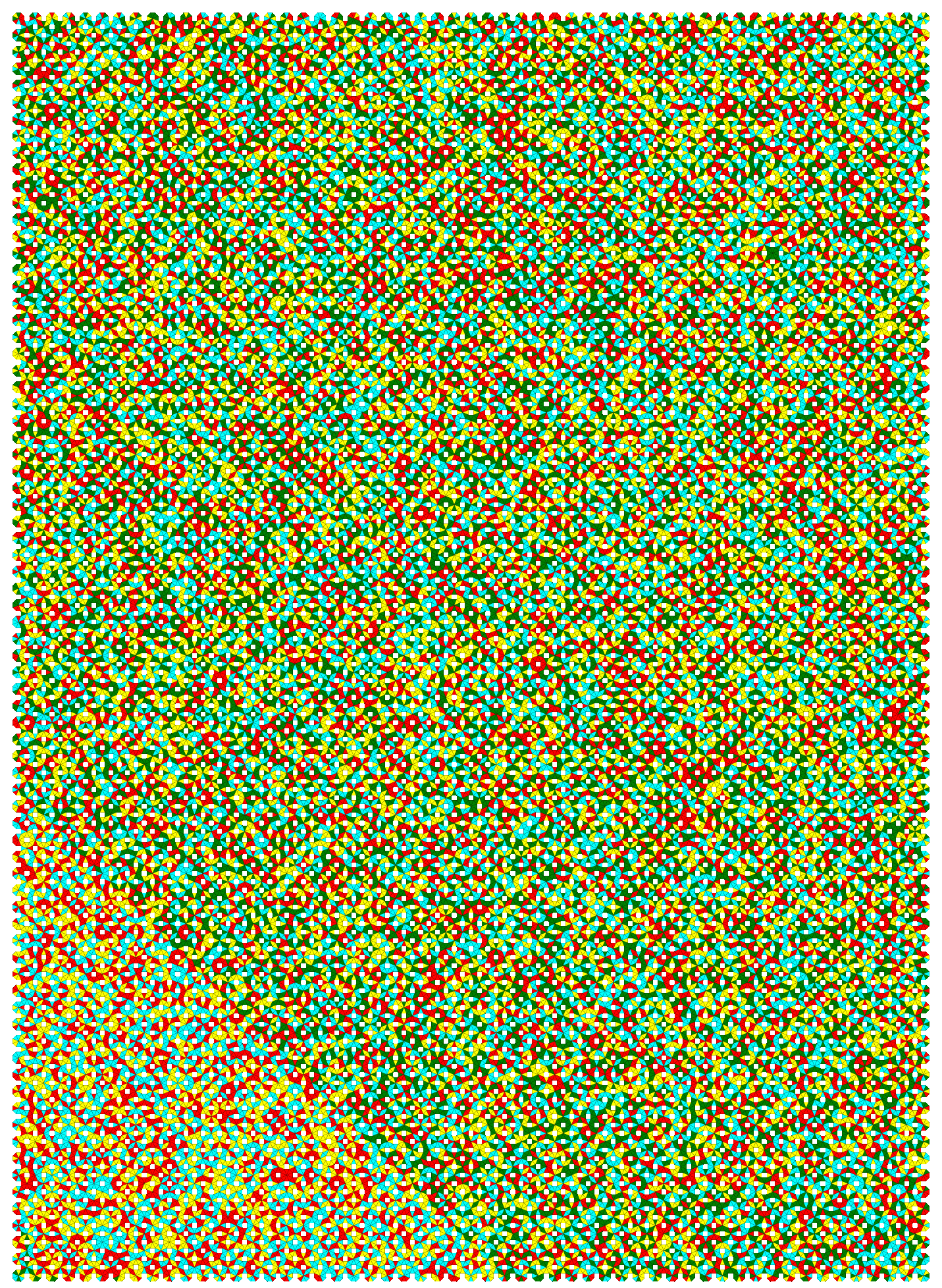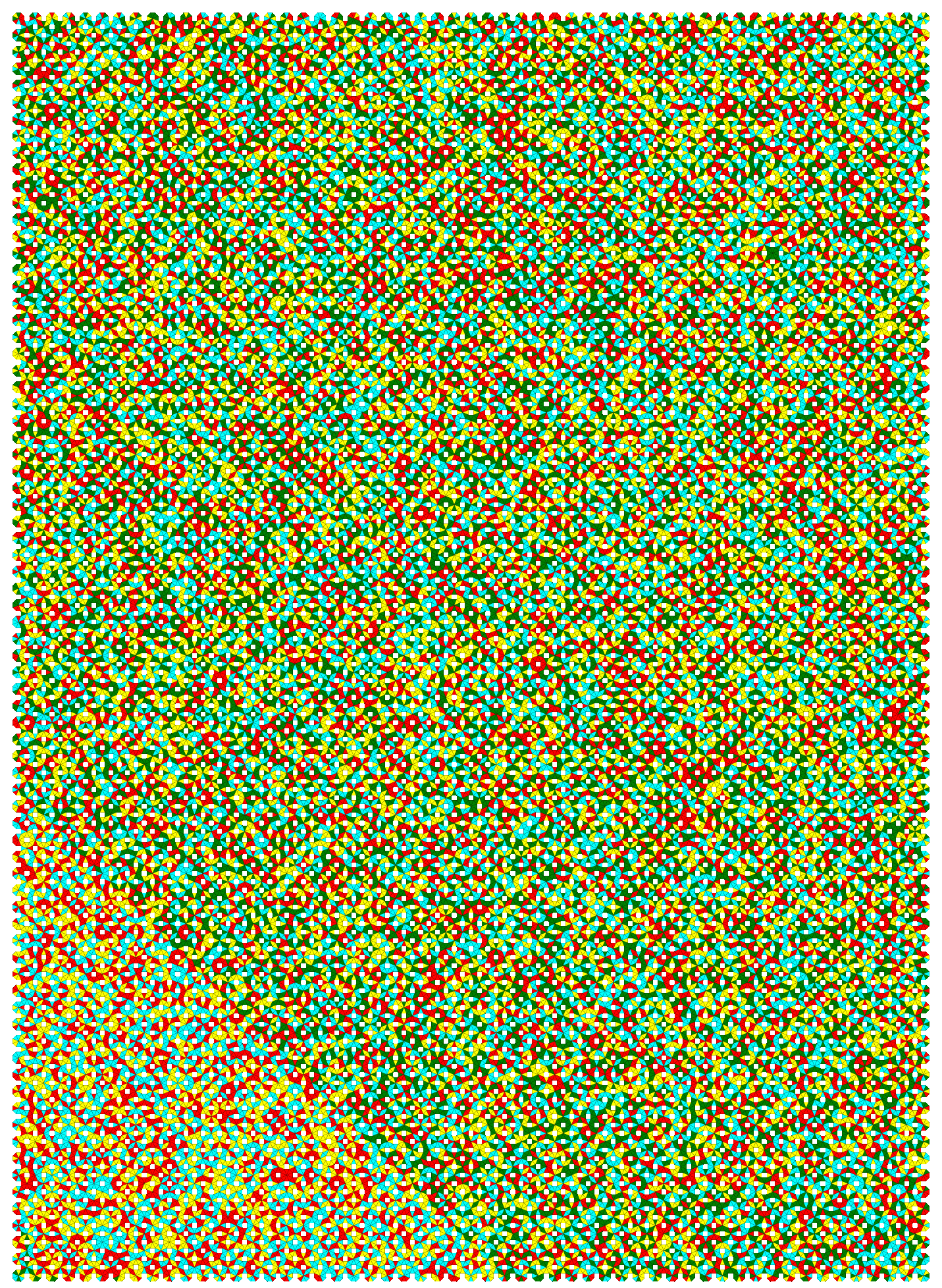4 Colors, No Restrictions, One-sided
If there are no restrictions we have 8230 one-sided pieces and 4435 two-sided pieces. Since 8230 = 2*5*823 we can try to cover rectangles of width 2, 5 or 10. It's no
problem to get solutions for the 2x4115 and the 5x1646 rectangles, because the rectangles are filled row by row and the length of the rows is rather small. For the 10x823 rectangles I needed a different approach. The first part was filled with octagons that have at least one edge with color 4. For the remaining area most pieces have only edges with color 1..3 and only few pieces with color 4. The SVG-file of this construction is here.
I also constructed a jagged rectangle of size 55x76 which was filled row by row at an angle of 45. The second part is located at the bottom left corner.
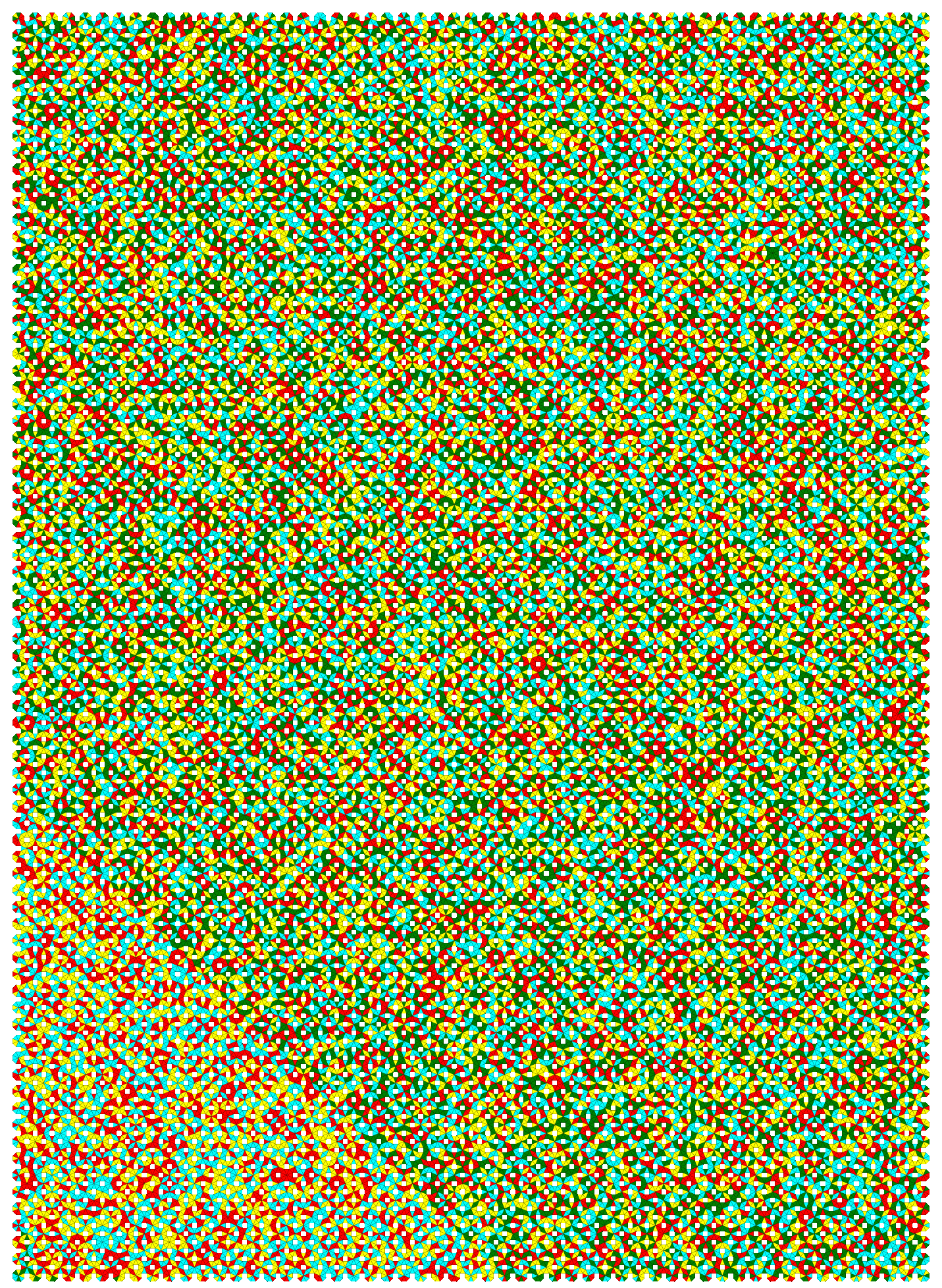
4 Colors, No Restrictions, Two-sided
The 4435 two-sided pieces can make a 5x887 rectangle. It's the only possible one, because 887 is prime and it's very easy to get a solution. A SVG-file is here.
The jagged rectangle of size 91x25 has longer rows, but since the pieces can be turned over there are more possibilities to finish the whole construction. Splitting the retangle wasn't neccessary.

4 Colors, 2 or More Colors on Each Piece, One-sided
Discarding same colored pieces 8226 one-sided pieces are left. Since 8226=2*3*3*457 rectangles of size 6x1371, 9x914 and 18x457 may be possible. Row
lengthes of 6 or 9 or even smaller are no problem for the backtracking process, but for the row length of 18 you must save pieces with color 1..3 for the last part, shown at the top.

4 Colors, 2 or More Colors on Each Piece, Two-sided
We have 4435-4=4431=3*7*211 two-sided pieces. Row lengthes of 3 or 7 aren't a problem, the 21x211 rectangle is shown.

Back
Home