3 Colors, No Restrictions
If all combinations are allowed we have 834 one-sided and 498 two-sided pieces. I solved rectangles of size 139x6=834 and 83x6=498, but
these rectangles with height 6 aren't easily to display. Therefore I made spirals of width 6, which have the same number of matching sides, and
solving these spirals was as easy as solving the rectangles.


3 Colors, At Least 2 Colors on Each Piece
Discarding same colored pieces 834-3=831=277x3 one-sided and 498-3=495=99x5 two-sided pieces are left. For both sets spirals instead of rectangles are shown.


The two-sided set can also cover a 45x11 rectangle with more matching sides than the spiral.

3 Colors, Exactly 2 Colors on Each Piece, One-sided
If we allow exactly two colors for each piece, solving get's a little bit more difficult. After each placement it seems to be usefull to check, if there are empty
places, which have more than two colors at their edges. In this case you must start early backtracking. Furthermore I got faster results, if at any stage only
rather few pieces (about 10) were tested and if no one fits, backtracking started. Here are three figures with the 102 one-sided pieces.

3 Colors, Exactly 2 Colors on Each Piece, Two-sided
With the 84 two-sided pieces rectangles of size 28x3, 21x4 and 12x7 are possible to construct.

3 Colors, 1 or 2 Colors on Each Piece, One-sided
If we add the three same colored pieces we have 105 one-sided and 87 two-sided pieces. With the one-sided set I made 35x3, 21x5 and 15x7 rectangles and a jagged rectangle.

Since 105=104+1 I constructed figures with rotational symmetry
and one piece in the center.

3 Colors, 1 or 2 Colors on Each Piece, Two-sided
With 84+3=87=3*29 pieces you can only cover a 3x29 rectangle. I added two jagged figures.

3 Colors, Ratio of Color Frequencies is 2:6
Given pieces with two colors out of three the sets with fixed frequency ratios of colors are three times as large as the set with only two colors given.
But the sets are still small and the constructions rather easy. For the color ratio 2:6 the number of one-sided and two-sided pieces is 24 and we can make 12x2, 8x3 and 6x4 rectangles.
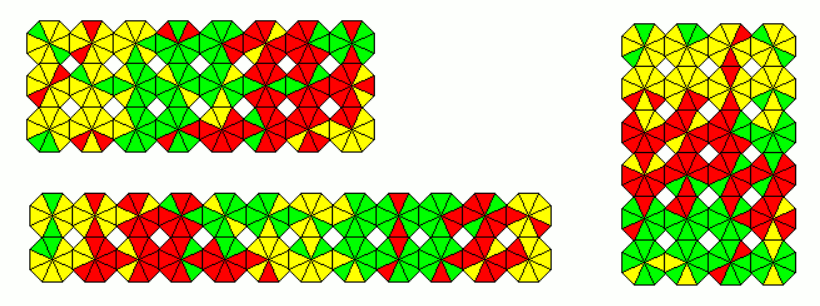
3 Colors, Ratio of Color Frequencies is 3:5
We have 42 one-sided and 30 two-sided pieces with color ratio 3:5. Possible are a 7x6 or 6x5 rectangle, respectively.

3 Colors, Ratio of Color Frequencies is 4:4
If four edges are colored with one color and four edges with a different one, we get 30 one-sided pieces enough for 10x3 or 6x5 rectangles. With the 24 two-sided pieces I made a 6x4 rectangle and a ring of size 5.

3 Colors, 3 Colors on Each Piece
If all three available colors are used at each piece, many frequency ratios are possible. I examined 2:2:4, 1:3:4 and 2:3:3. The sets are larger and
dead branches in the search tree don't occur very often. But the display of the results don't show any structure like those with the two-colored pieces.
3 Colors, Ratio of Color Frequencies is 2:2:4
These sets are slightly smaller as the other ones. As an example a 18x9 rectangle with the 162 one-sided pieces and a 11x9 rectangle with the 99 two-sided pieces is shown.

3 Colors, Ratio of Color Frequencies is 1:3:4
The 210 one-sided pieces are shown as a 21x10 rectangle and the 114 two-sided pieces as a 10x6 rectangle.

3 Colors, Ratio of Color Frequencies is 2:3:3
For this ratio of color frequencies we get 210 one-sided and 114 two-sided pieces. Surprisingly these are the same numbers as for the 1:3:4 ratio.
I constructed the same rectangles, 21x10 with the one-sided pieces and 10x6 with the two-sided pieces.

Back
Home
















