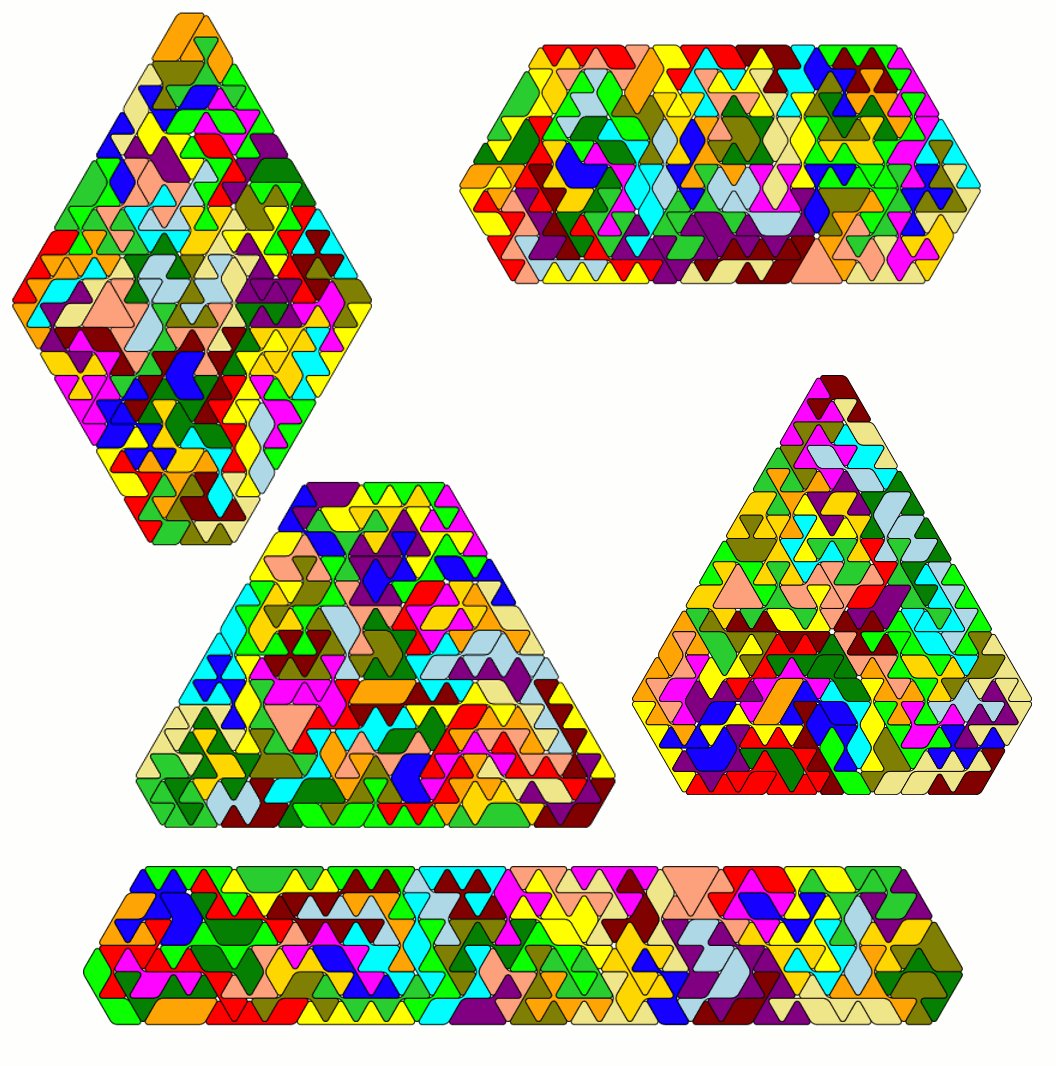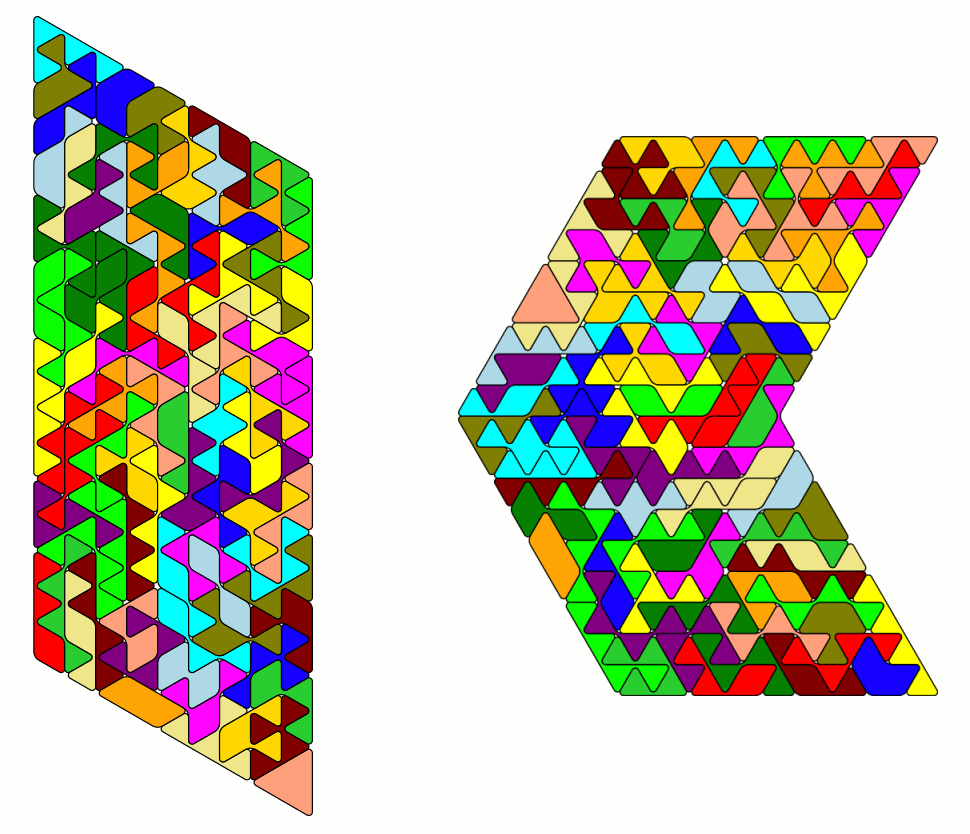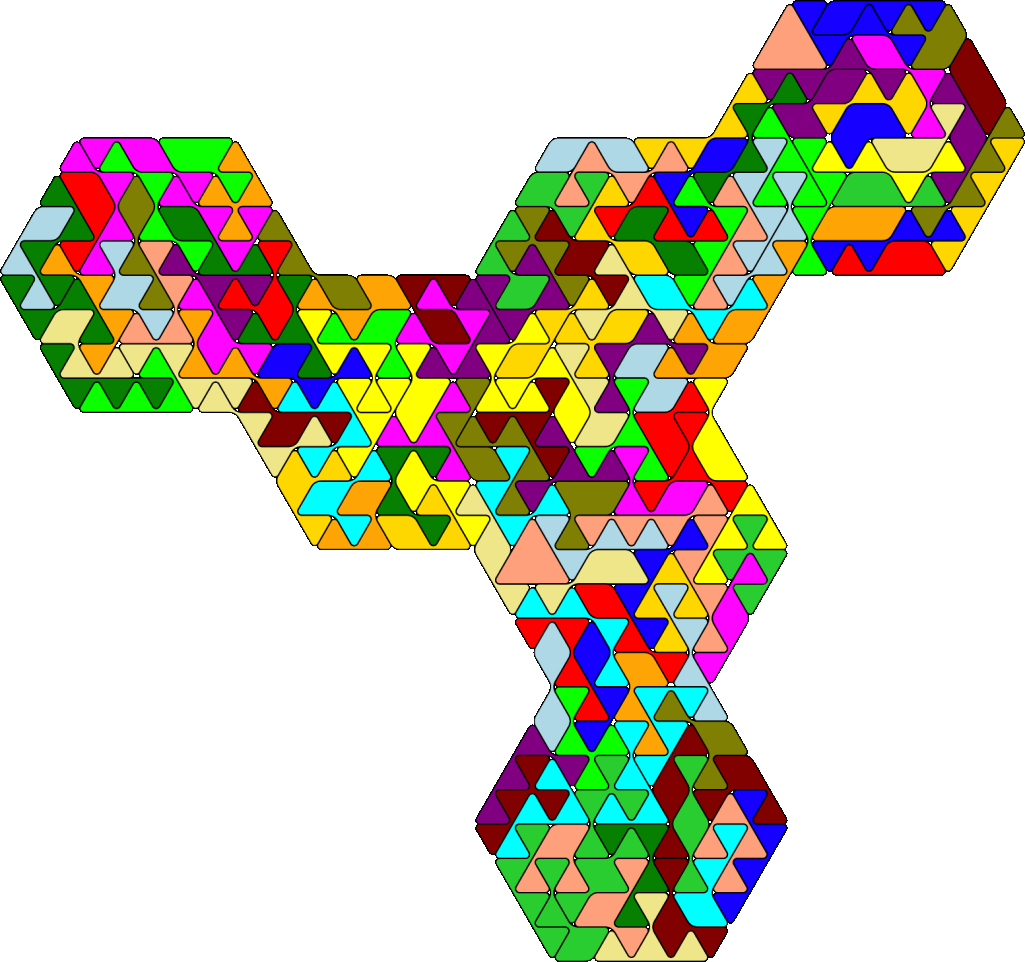Bridged Tetriamonds
Two-sided Pieces
The picture shows the 82 bridged tetriamonds as real pieces. First I printed the top and the bottom face of each piece
with a 1mm thicker edge. Then both parts were glued together with two 2mm thick magnets inside. This way it is easy
to fix the pieces on iron boards.

To spot a special piece in the set you can divide the set into subsets with equal numbers of bridges.
If there are more than one bridge you can count where and how often each kind of bridge exits. This depends on the
number of connected triangles and the angles at both sides of the bridge.
Unfortunately there is a parity problem with the pieces. We can call a piece odd, if the number of white triangles under
checkerboard coloring is odd. Because the number of odd pieces is odd constructions with two orthogonal axes of symmetry
aren't possible.
The figure with triangle symmetry shown at the initial page was constructed more than a decade ago. Now I looked for
convex polygons some of them with one mirror symmetry.
Starting with a large triangle of size g you can cut three
triangles of size a,b,c >= 0 at the corners. The following neccessary conditions must hold:
- g*g-a*a-b*b-c*c=328 (use all pieces)
- d=g-a-b >= 0
- e=g-b-c >= 0
- f=g-c-a >= 0
- (g-a-b-c) mod 4 = 2 (parity condition)
Now a,d,b,e,c,f are the side lengths of an hexagon if all values are greater than 0.
A side length of 0 indicates a 60 degree angle between the neighboring sides giving one corner less.
- Symmetric hexagons: 4-11-4-14-1-14; 2-15-2-12-5-12; 10-3-10-12-1-12; 4-15-4-6-13-6; 2-27-2-4-25-4
- Asymmetric hexagons: 10-8-3-16-2-9; 14-7-2-20-1-8;
- Pentagons: 8-6-7-14-0-13; 20-6-1-26-0-7
One symmetric hexagon is shown as construction with the real pieces:

Here are all symmetric hexagons.
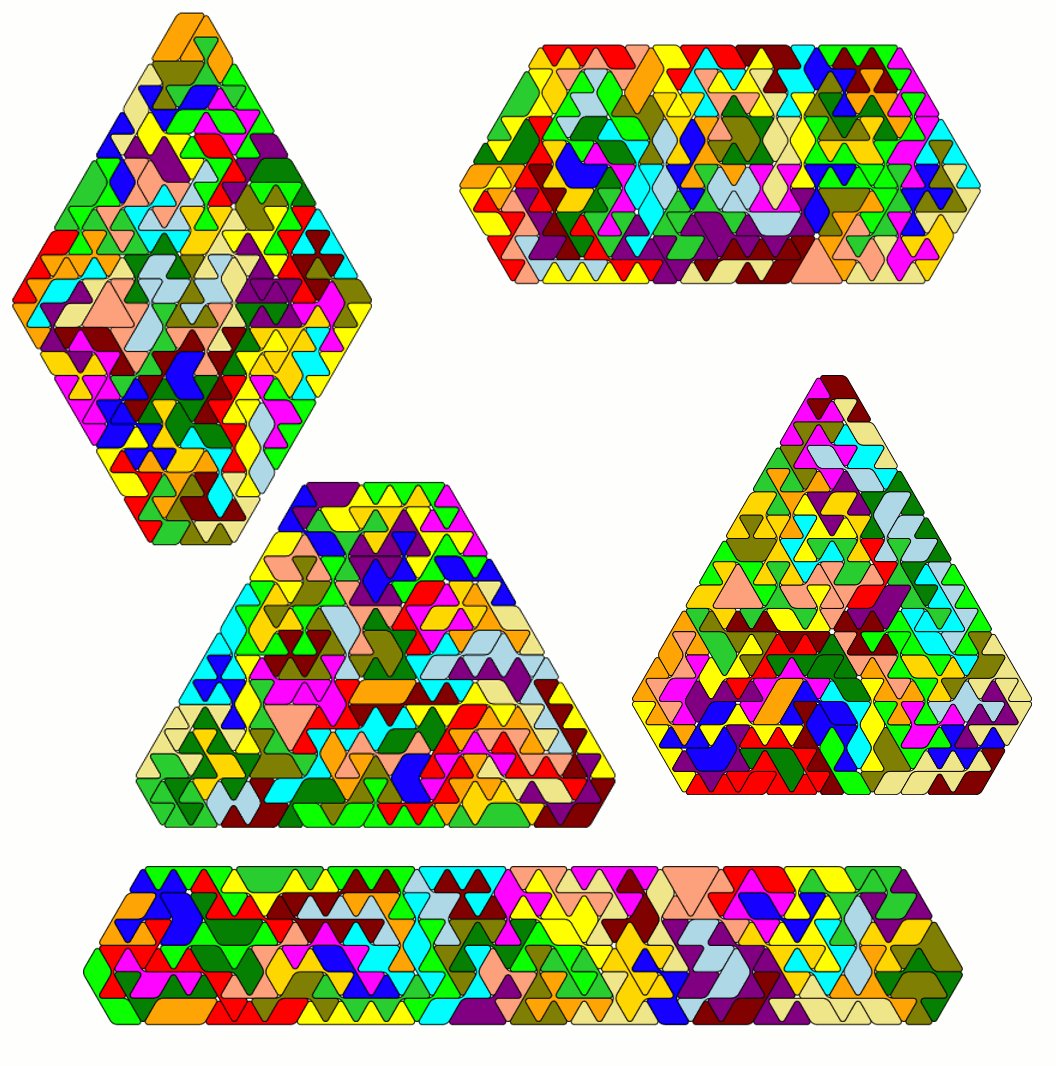
At last I solved one pentagonal figure. I think solutions exist for all other listed polygons.
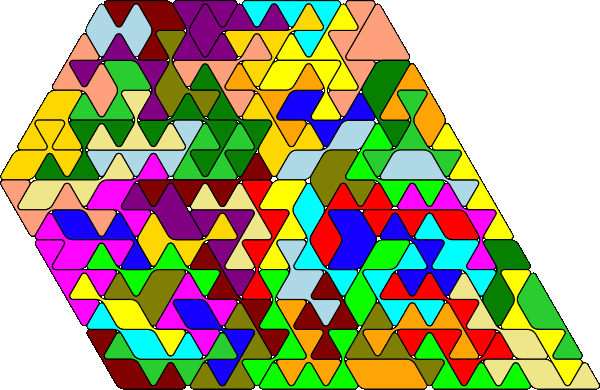
It seems to be possible to construct 9-fold replicas of some of the pieces. 81 pieces must be used and one
piece is left. This is odd if the replicated piece isn't odd and vice versa. First I tried to replicate the pieces
without bridges. This is the triangle shown with the real pieces.

The parallelogram and the chevron are also possible.
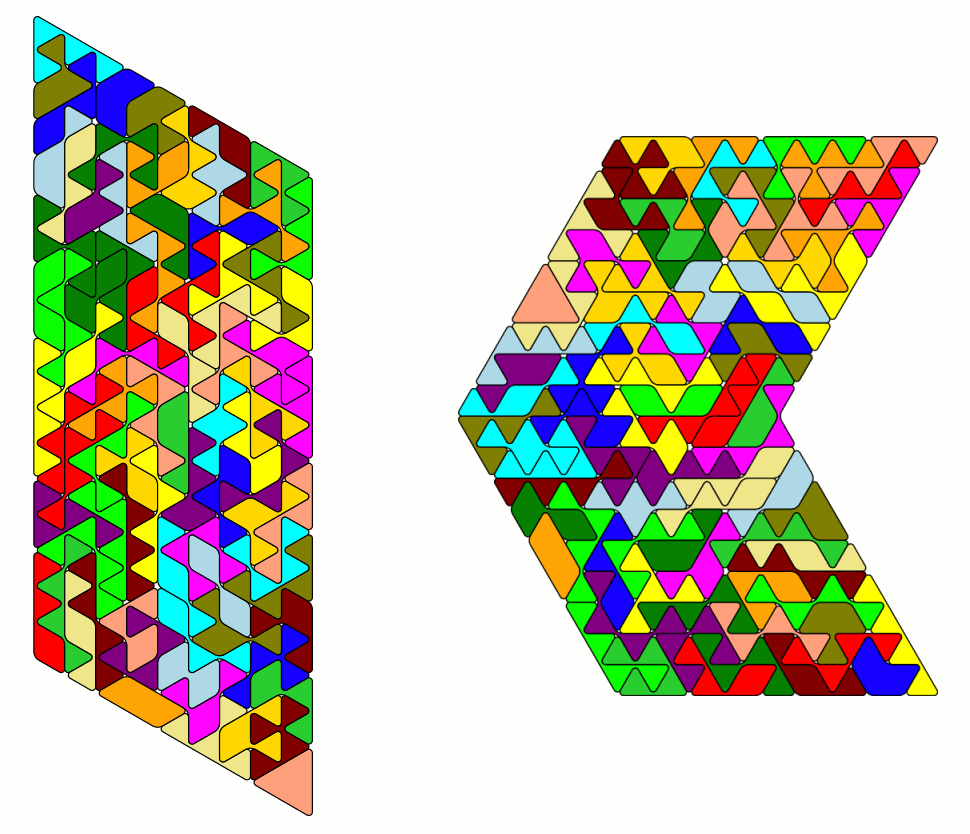
So far I constructed the 9-fold replica of a piece with only one bridge.

One-sided Pieces
Here are the 143 one-sided bridged tetriamonds with a total area of 572 triangles.

A SVG-file to print or cut the pieces is also provided.
Since the number of odd pieces is odd we have the same parity issues with this set as with the double-sided one.
So we can't get constructions with two axes of mirror symmetry. But there exist a lot of convex polygons which can
be made.
For neccessary conditions look at the double sided set with total area condition
changed to g*g-a*a-b*b-c*c=572.
If all values of a,d,b,e,c,f are greater than 0 we get a hexagon, one zero indicates a pentagon and
two zeros a quadrilateral.
- Trapezium: 2-22-0-24-0-22
- Asymmetric pentagons: 10-14-2-24-0-16; 11-10-6-21-0-16;14-10-4-24-0-14; 13-6-10-19-0-16; 18-10-2-28-0-12;
16-2-14-18-0-16; 22-2-10-24-0-12; 30-2-7-32-0-9; 32-6-2-38-0-8; 32-2-6-36-0-8;...
- Symmetric hexagons: 16-8-6-18-6-8; 24-8-2-30-2-8
- Asymmetric hexagons: 6-15-4-20-1-18; 8-12-6-18-2-16; 12-12-3-22-2-13; 12-8-8-18-2-14;12-7-10-14-5-12;
13-6-6-15-6-10; 18-6-7-20-4-9; 20-6-6-22-4-8; 33-4-4-35-2-6
This is the trapezium.

I constructed only one asymmetric pentagon. Another one can be made by joining the two rhombs
where one corner is cut.

Here are two asymmetric hexagons.
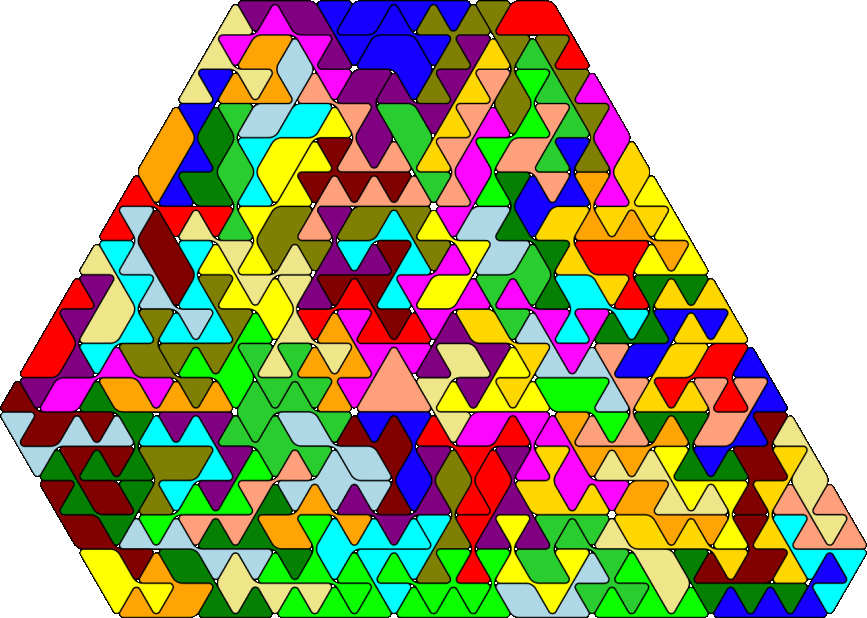

There are two symmetric hexagons one of them is shown with the real pieces printed with a 3d-printer. To get no
problems by assembling the pieces you have to print them with a small inset.


If we add another odd pieces to the set for instance the triangle shaped piece, the number of odd pieces is even and no parity problems arise.
Furthermore we have 144 pieces which is perfect to look for 12-fold replicas of some pieces. If we add
the triangle shaped pieces at the top of the trapezium shown above, one replica is found. With the
following constructions it's possible to replicate pieces with at most one bridge.

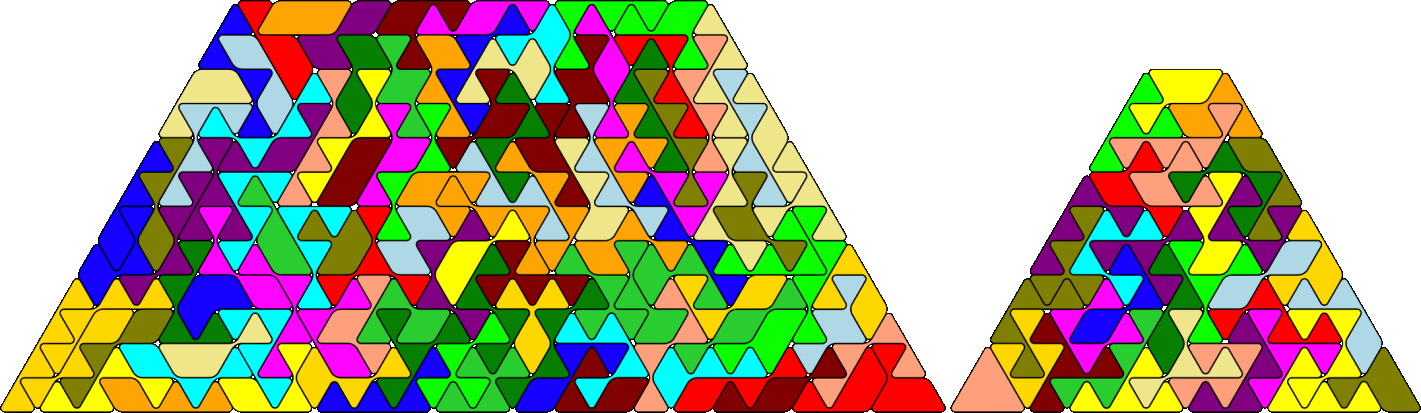
If we use the extended set constructions with hexagonal symmetry can also be made.

We can also make 4-fold replicas of hexhexes, if we replicate all six combinations of trihexes. These replicas can be
joined to get hexhexes.
There are only few hexhexes, which can't be replicated this way, but all solutions seem to be possible. An example
with triangular symmetry is shown.
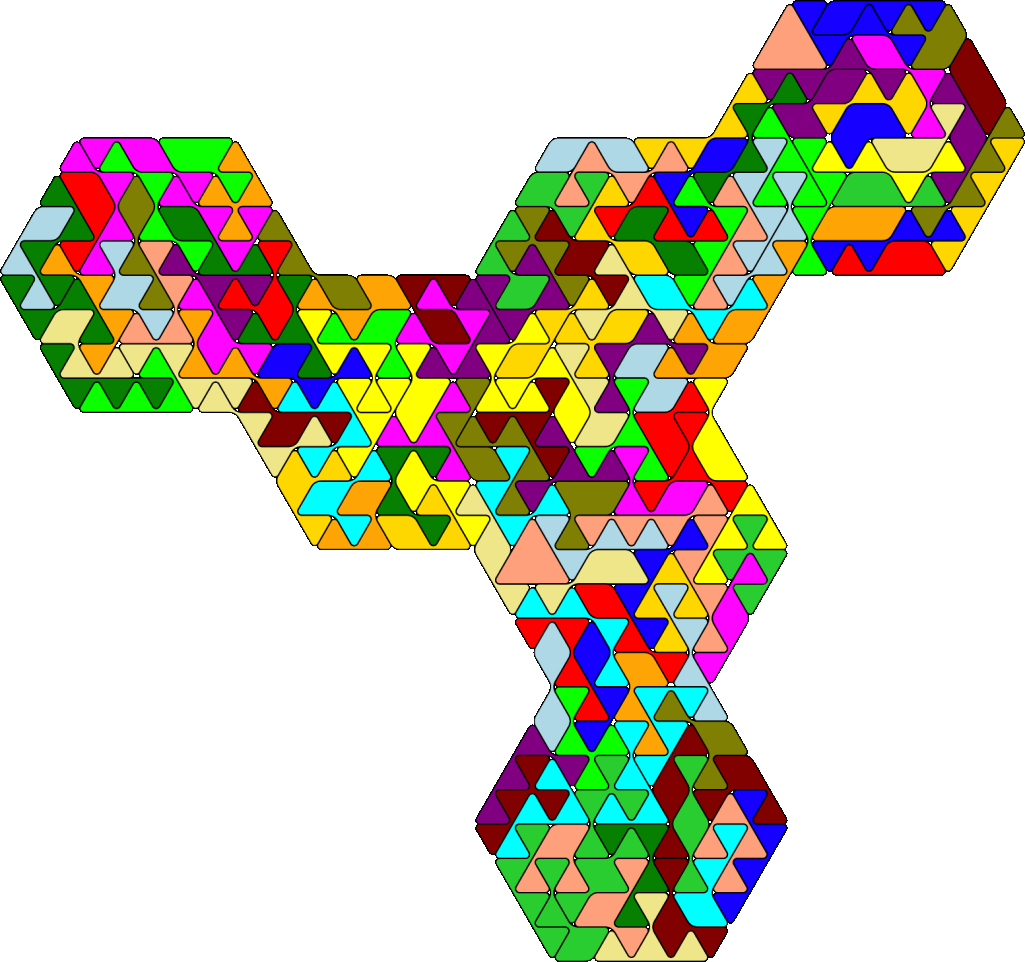
Back
Home