Bridged Diamonds & Triamonds
Two-sided Pieces
There are three bridged diamonds with an total area of 6 triangles. Adding these pieces to the bridged triamonds
some more symmetric constructions are possible. For handsolvers this set seems to be a little bit easier.

Three convex polygons can be made.

Some figures with triangle symmetry are shown.

With a hexagonal hole we get more symmetric constructions

Instead of the hexagon hole in the second figure it's possible to get holes shaped like all other
ordinary hexiamonds. The solutions are here .
One-sided Pieces
The 19 one-sided pieces can cover an area of 54 triangles. This is just enough to get a regular
hexagon without an hole. The printed pieces are placed on a light panel so that the borders between the
pieces are better to be seen.

I looked for other convex polygons and got four additional constructions with different symmetries.

Since 54 is a multiple of 3 figures with triangle symmetry are also possible.

Examples with rectangle symmetry are shown below.
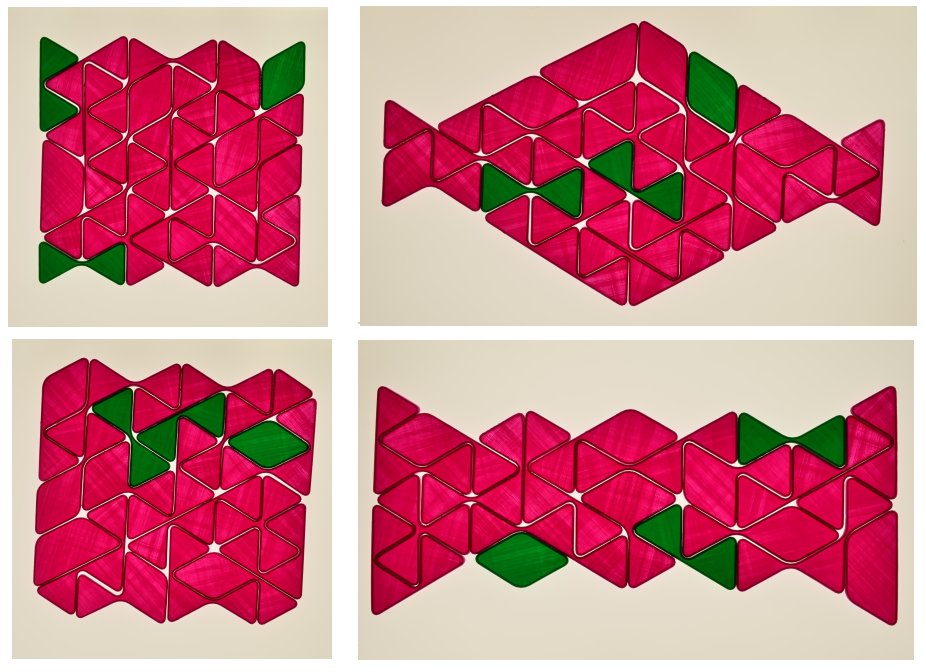
At last I added another construction with hexagonal symmetry.

Back
Home









