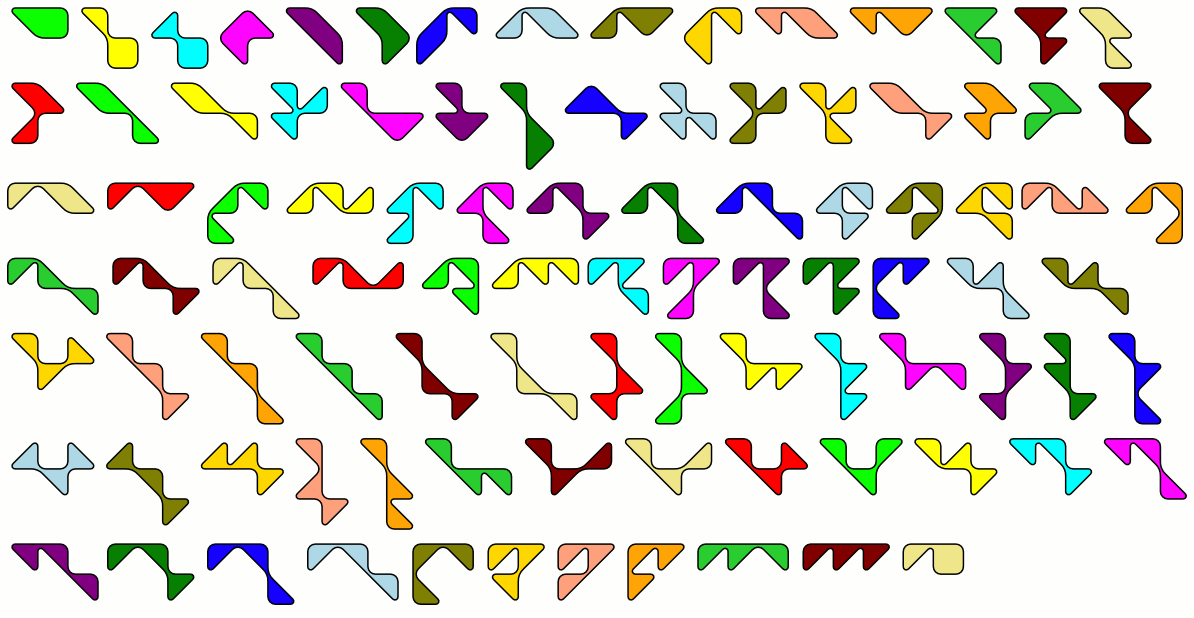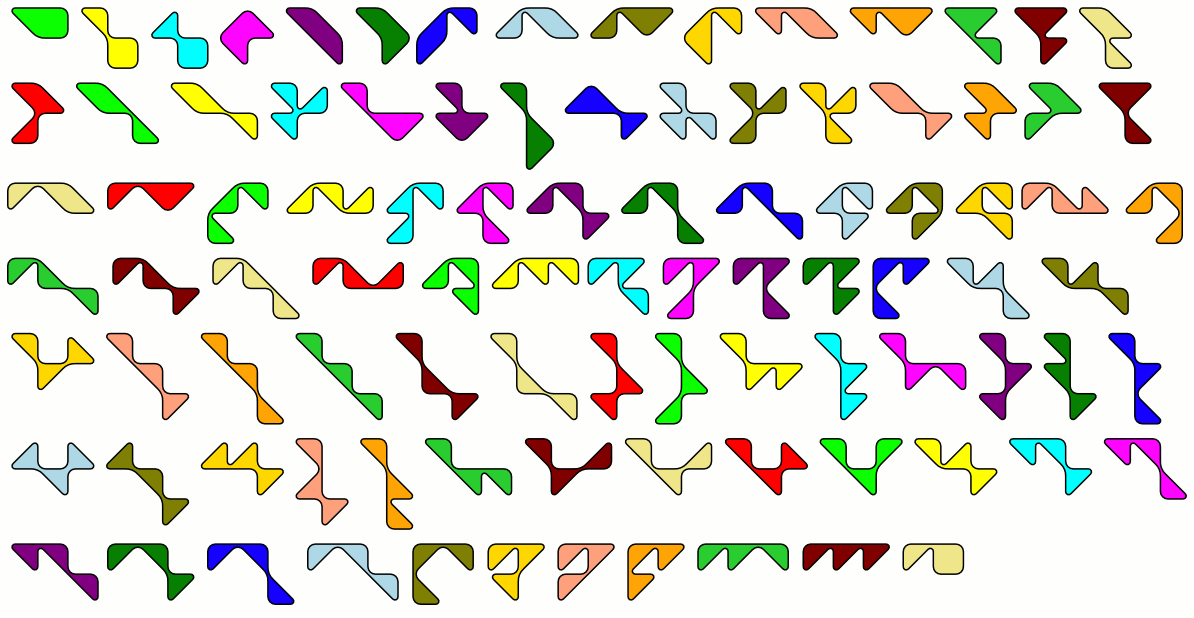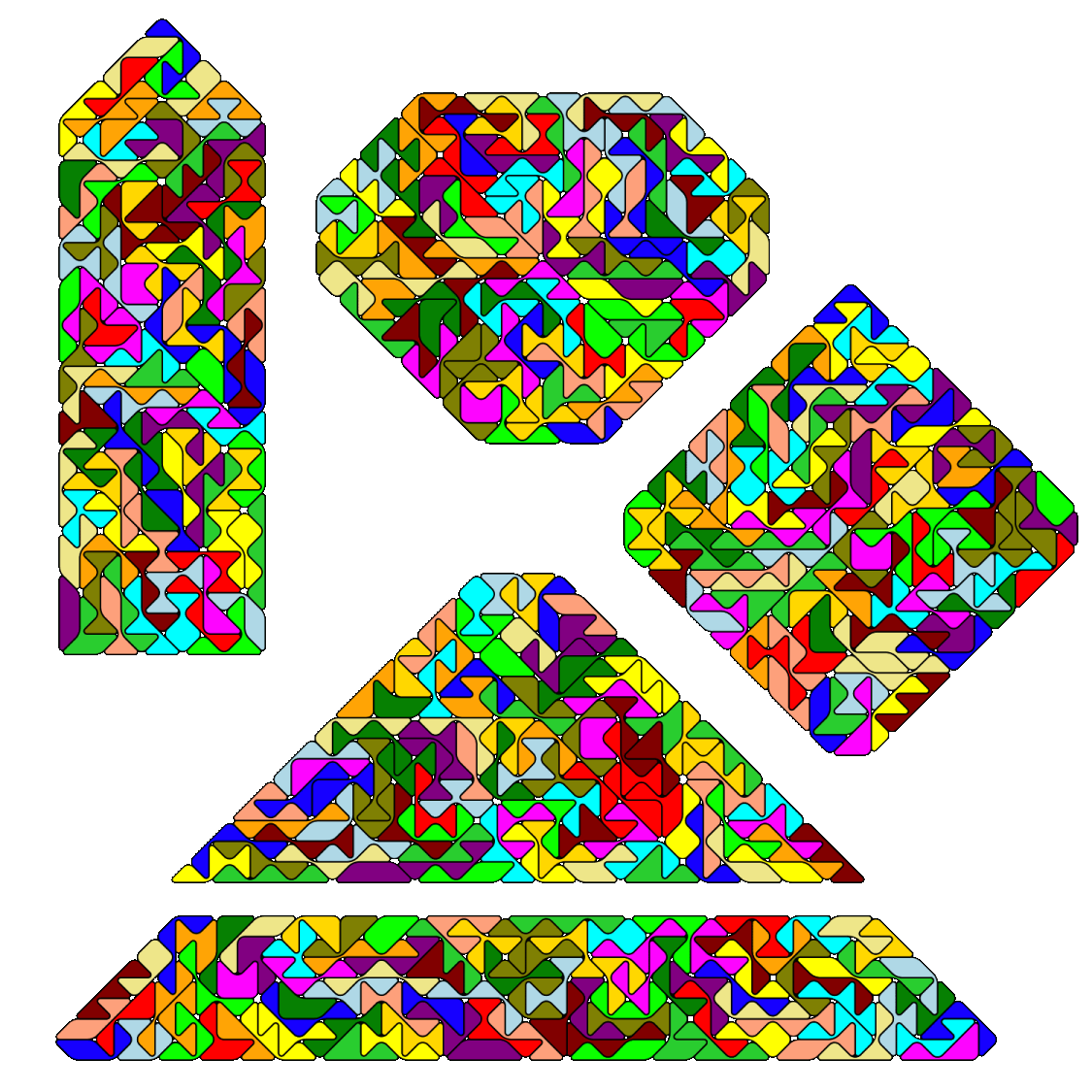Bridged Tritans
Two-sided Pieces
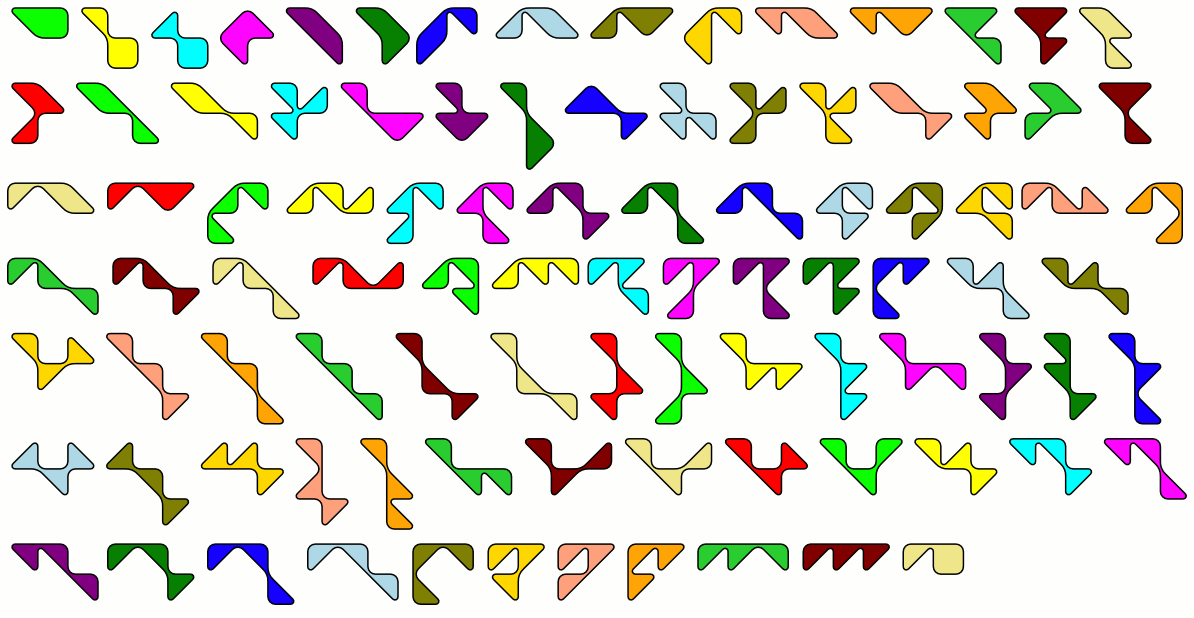
Here are the 95 two-sided bridged tritans. You can use the SVG-file to cut or print the pieces.
Since each triangle has one hypotenuse each piece has one or three of them at its border.
Therefore the total number of hypotenuses at the border is odd and constructions with two axes of symmetry aren't possible.
But a lot of convex polygons can be made and some of them have a mirror symmetry. Shown are symmetric polygons
with 4, 5, 6, 7 or 8 corners. The total number of hypotenuses at the border of the polygons is always odd.
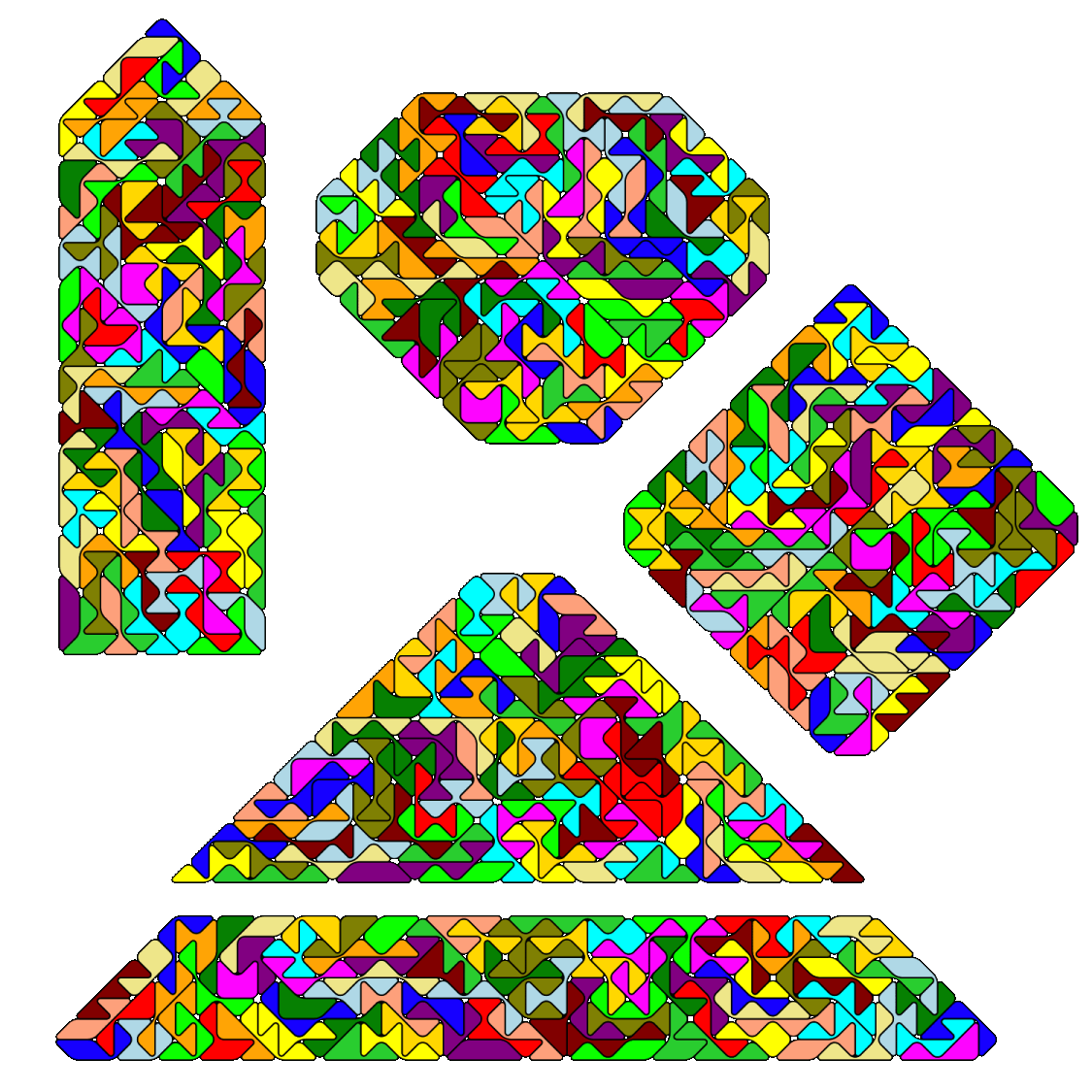
The heptagon is essentially a 12x12 square with one triangle removed from three of the four corners.
You can join the three triangles to get a bridged tritan and place a hole shaped like this piece in
the center of the square. These were the first figures I made with this set. An example with the real pieces is
shown on the title page. The computer solution were found rather fast, but assembling the real pieces takes some time.
Three further computer solutions are shown.

If you take the trapezium above and extend it by a small triangle of size 2 you get a large triangle of size 17.
Leaving a triangle hole of size 2 in the center of the large triangle you have a similar hole figure.

One-sided Pieces
We have 179 one-sided bridged tritans, and the total number of hypotenuses at the edges of the pieces is odd, too.
Therefore construction with two axes of symmetry aren't possible. As with the the two-sided pieces I tried
to find convex polygons with reflection symmetry. For a trapezium with parallel sides made from hypotenuses we have
179*3=a*a - b*b. The solution a=91, b=88 needs 91+88 = 179 hypotenuses at the border, but the pieces can
only contribute about 155. Construction for symmetric convex polygons with 5,6,7 or 8 corners are possible. Due
to the large number of pieces the whole figure had to be divided up in three or four parts and it lasted a little bit
longer to find the solutions.

Though neither a rectangle nor a triangle can be made with the whole set combinations of both figures are possible.

 Back
Back
Home