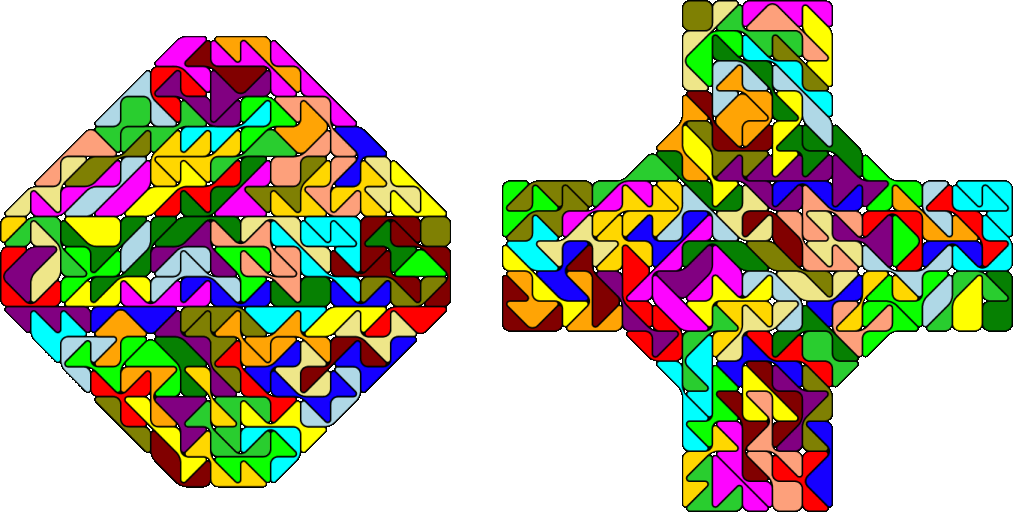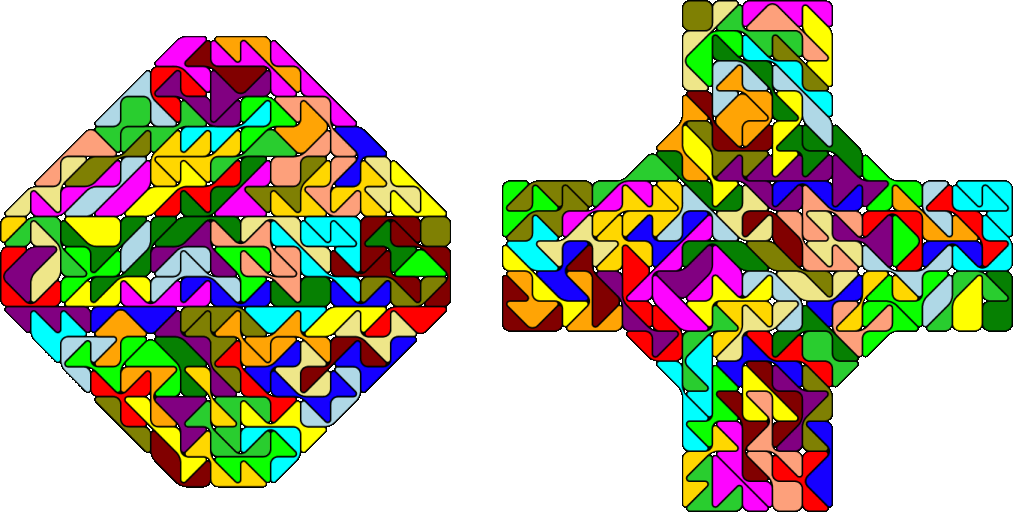1..3 Bridged Tans
Two-sided Pieces
Adding the ditans and a single tan to the set of tritans we get a pretty nice set of 106 pieces
with an area of 153 squares and no parity problems. Constructions with two axes of symmetry and symmetry under
90 degree rotation are possible. In the last case the center of symmetry must be the center of a square in the grid.
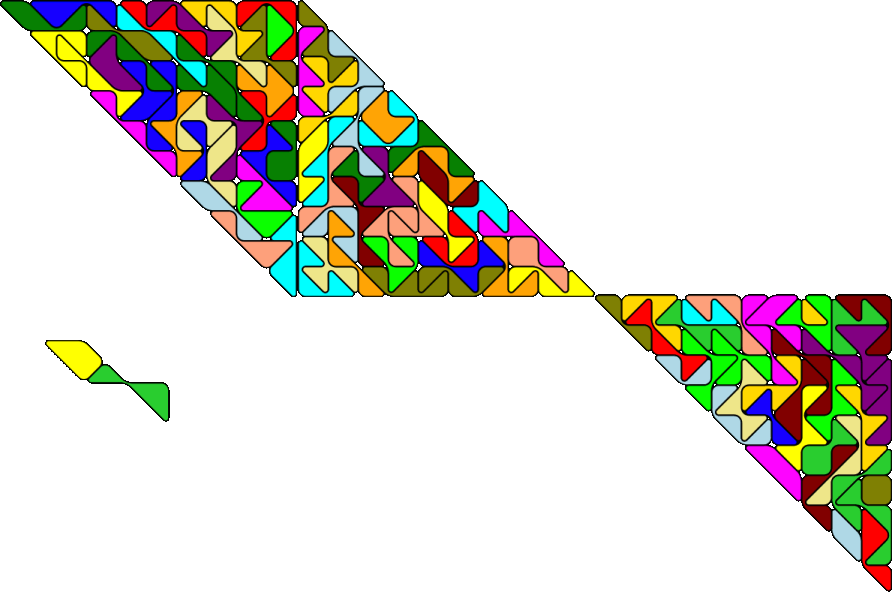
Here are an octagon and a cross.
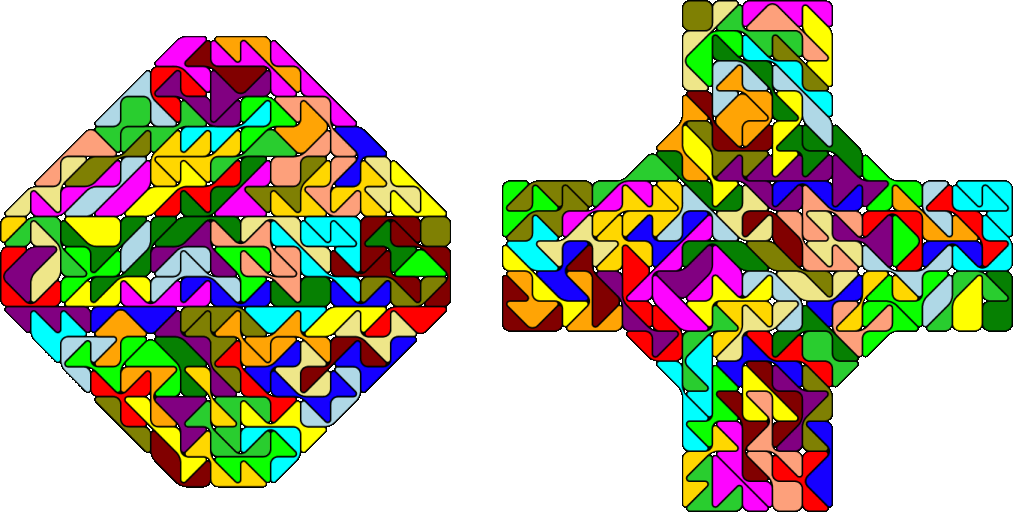
Inside the octagonal ring other ditans can be placed, but in this case some or all symmetry is lost.
Without the parity problem you can also make a rectangle.

Because there are 306 = 3*102 triangles in the set it seems to be possible to simultaneously replicate the tritans
by a factor 10 and a factor of sqrt(2). Two examples are shown.
One-sided Pieces
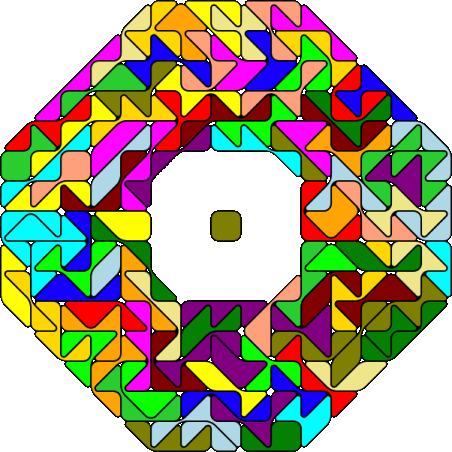
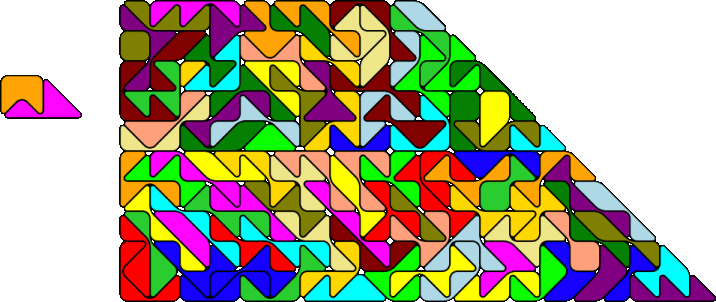
There are 195 pieces with an area of 284 squares and no parity problem. I constructed two figures
with square symmetry: an octagon and a square with a square hole.
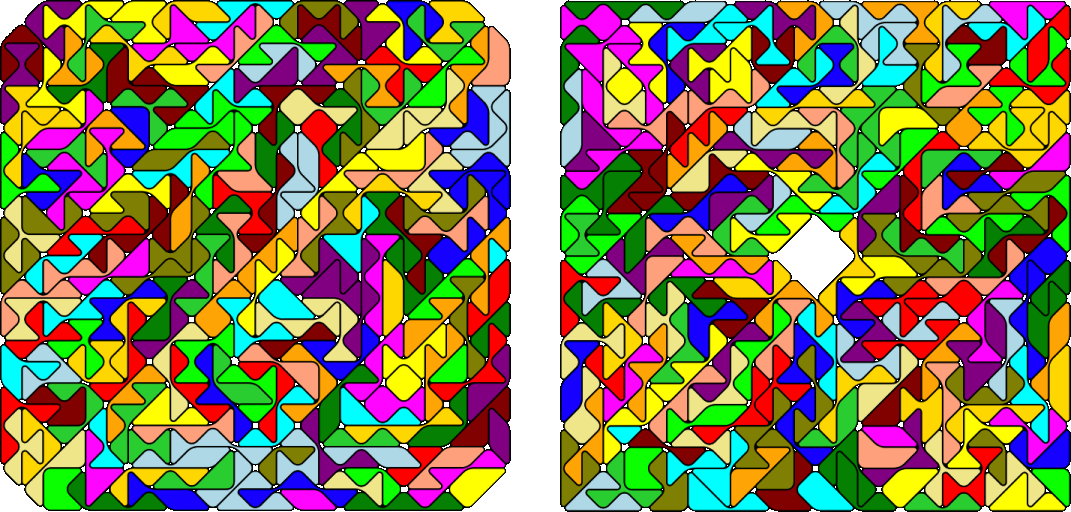
Two copies of each figure scaled down by a factor of sqrt(2) are also possible.

Back
Home