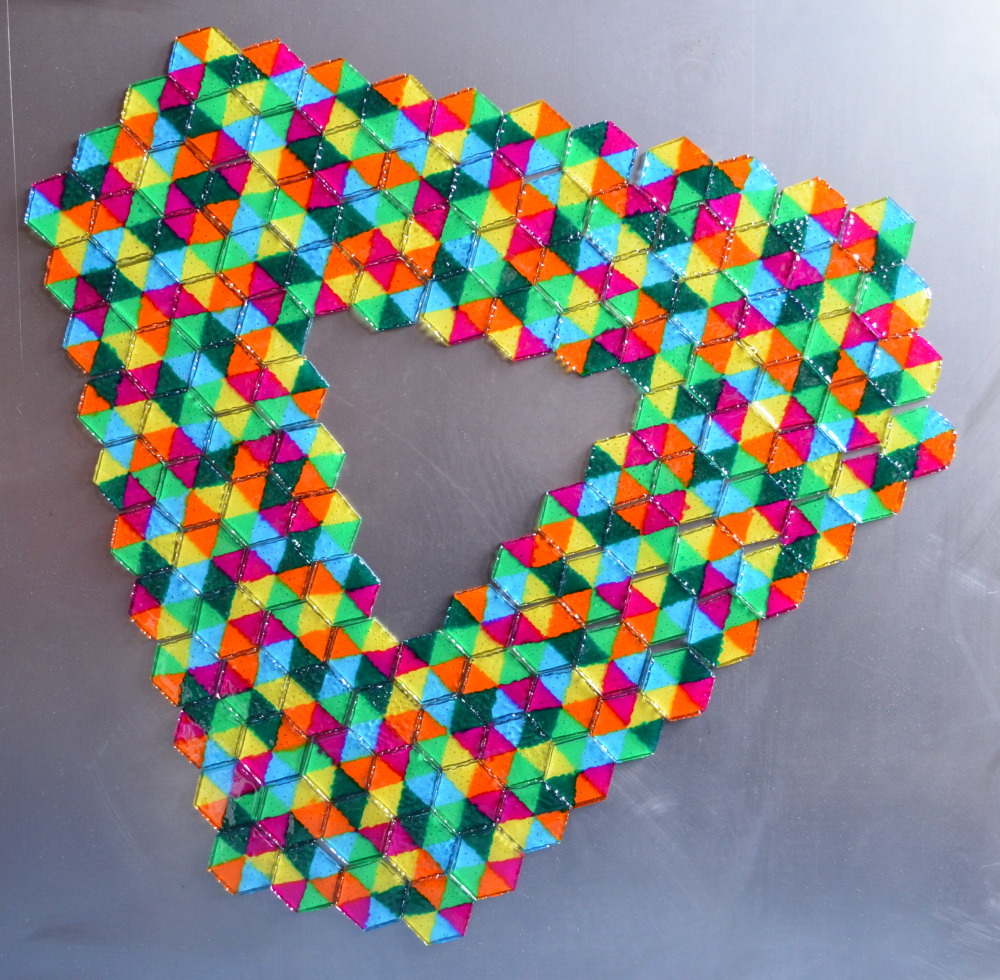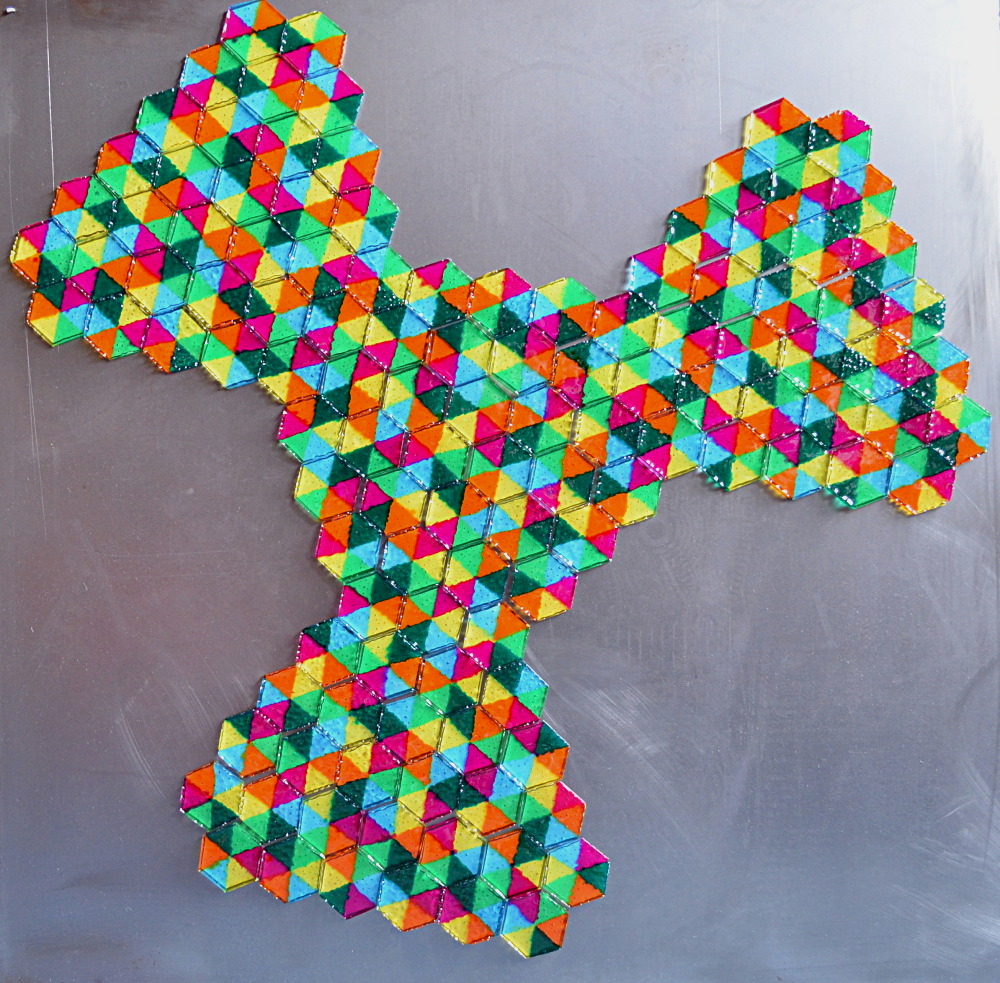Colored Hexagons
After I had made 120 one-sided hexagons from hard foam with six different colors at the edges, I tried
another method to produce the pieces using some kind of melt granulate.

The hexagonal cast was divided in six triangles by card board and differently colored granulate was filled
into the sections. Then the card board was removed and the granulate melted.

The following star is an example for a construction symmetric under 60 degree rotation
with six axis of mirror symmetry.

There is another kind of symmetry for the colors. You can rotate each piece by 180 degree
around the center of the star and get a twin piece with fuchsia and dark green triangles swapped. This
property was used to get the whole construction after half of it is solved with only one piece of each pair.
To avoid the hole in the star I constructed a jagged hexagon with two axis of symmetry.

Parallelograms of size 8x15 and 10x12 and a semiregular hexagon with edges of size 4-8-9-4-8-9 don't
have any holes neither and are symmetric under 180 degree rotation. Therefore the above mentioned method can
also be used.



Unfortunately a kind of rectangle with no hole isn't possible
but with a single hole at the center it's no problem.

What about constructions with no symmetry under 180 degree rotation?
If there are sharp corners, hexagons at these positions have only two edges to match and can
be places at last. In this case the computer program produced solutions after some time.
But for constructions like the triangular ring shown below, there was no chance. I had to rethink my algorithm.
Take triplets of pieces like a-b-c-d-e-f, a-b-c-e-f-d and a-b-c-f-d-e. The colors a,b,c are fixed and the colors
d,e,f can be transformed by an even permutation. This way you can get 40 triplets of pieces and
it's possible to solve a third of the construction with one piece of each triplet. Then the two other thirds
are given by tranformation. Additionally the touching pieces
of two different thirds must match. Now solutions were found in seconds.
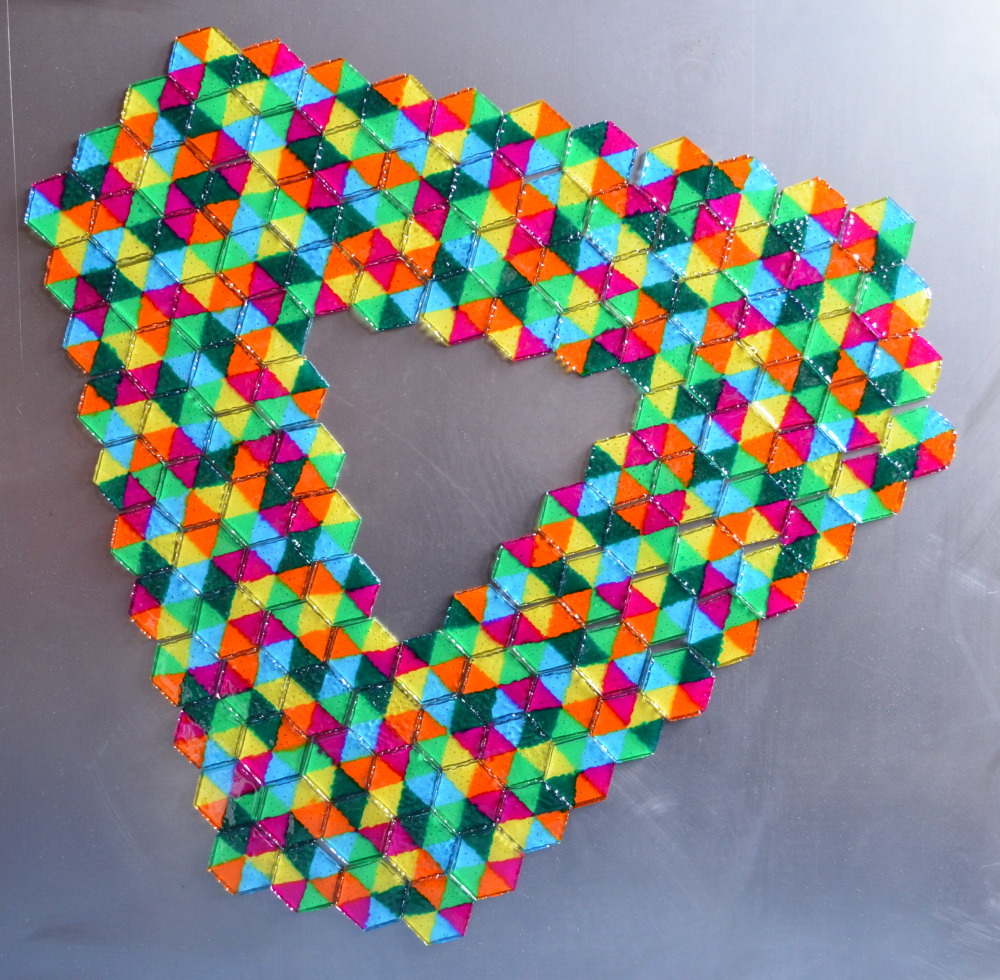
Here are three jagged triangles, which are combined to get a propeller. Because two parts only touch at one
edge it's easy to meet the color match.

At the center of the following construction three pieces of three subsets meet and the matching color
must not be one of the fixed ones in each triplet. Perhaps you'd like to spot the separating lines
between the three parts.
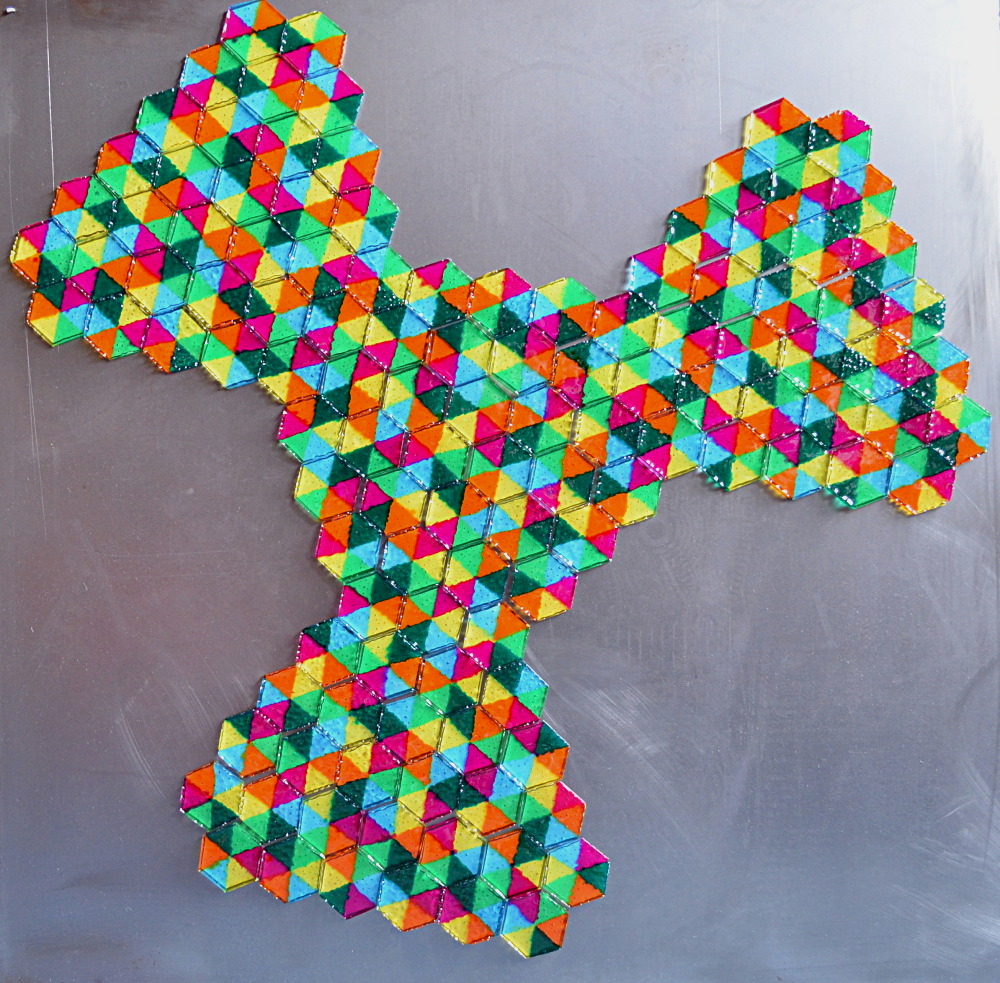
Index