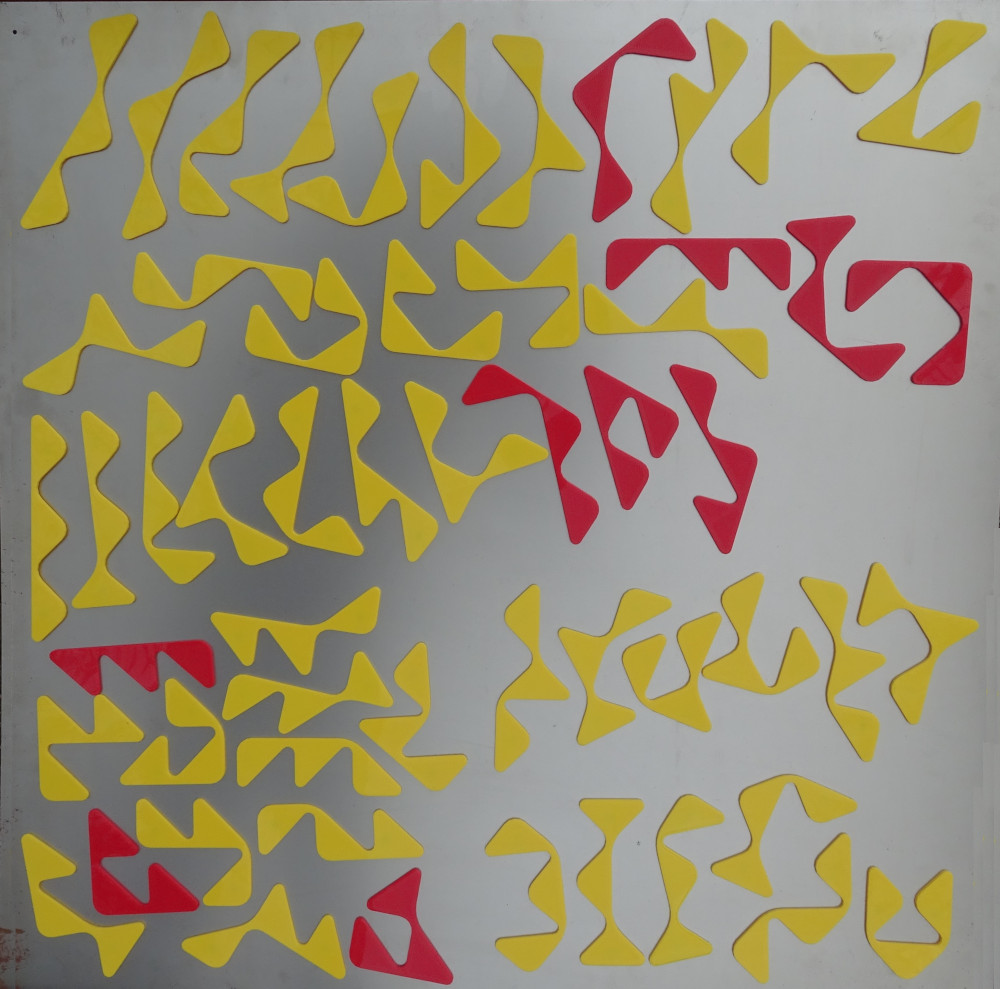Bridged Polytans of Order 1..3

Above there is a construction with the two-sided bridged polytans of order 1..3. A definition
of the pieces is here. We have one single tan, 10 ditans and 95 tritans with a total area
of 1+10*2+95*3 = 306 tans or 153 squares.
For each piece I printed two mirror parts with a slightly higher edge and stick the two parts
together with two small magnets inside. This way I could put the pieces on an iron board and it was easy
to carry away a whole construction. The colors are without meaning. I only wanted to use my remaining
red filament.
First I sorted the pieces due to their number of tans. To sort the ditans they got names like triangle,
square, parallelogram, hourglass, hills, tie, groove, buoy or saw. So it was easier to identify them.
For the tritans you can examine which ditan is part of them and get some subsets. Here are the
pieces in a not so perfect order.

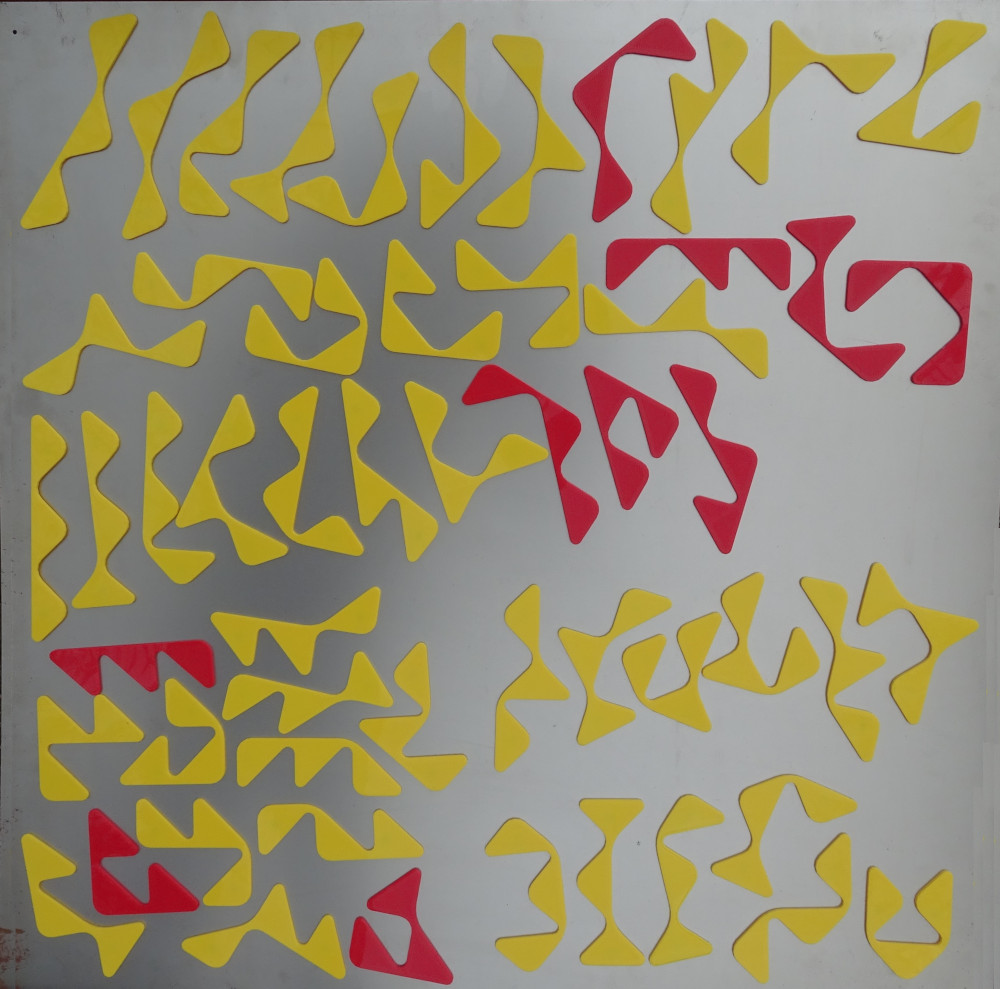
The cross shown in the title is a 13x13 square with four 2x2 squares removed from the four corners.
You can also remove the 2x2 squares from inside the large square. Two examples are shown.


We get the maximum of 32 triangular holes inside a 13x13 square by the following figure.

If you don't like holes you might prefer convex symmetric figures like a hexagon or an octagon.


Multiple squares are also possible:



To replicate some tritans we can make three triangles 10 times as large as a single tan with two
tritans left. Before the last triangle is constructed, you can keep back two tritans, which can
be used to make a replica by a factor of sqrt(2). Then you have two simultaneous replicas. In the
following examples the first two triangles are all the same, but for the third one there are two
different solutions.




At last a ring with a single tritan in the center is shown. You might choose any other tritan as well.

Index